Klurigt nr 25 (lösningar)
"Internationella problem Cadet (gy) 2007 "

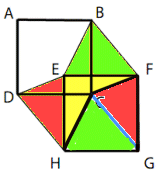
Tärningarna

Svar:
a) 27 tärningsögon   b) 3 resp. 5 tärningsögon
 Lösning:
a) Sammanlagda antalet tärningsögon på två motsatta sidor är alltid 7.
På en tärning: 3 . 7 = 21
På två tärningar: 2 . 21 = 42
Dolda "ögon": 42 - 1 - 2 - 4 - 6 - 2 = 27
b) För den högra tärningen är det enkelt: 7 - 2 = 5
Om man vrider den högra tärningen så att den kommer i samma läge som den vänstra tärningen, måste sidan med fyra tärningsögon hamna på den vänstra dolda sidan.
7 - 4 = 3
 

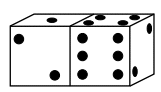
Kvadraterna

Svar:
34 cm2
 Lösning:
Den stora kvadratens sida är (3 + 5) cm = 8 cm
Arean är 8 . 8 cm2 = 64 cm2
Var och en av de fyra rätvinkliga trianglarna har arean
3 .  5/2 cm2 = 7,5 cm2  Sammanlagt: 4 .  7,5 cm2 = 30 cm2
 64 cm2 - 30 cm2 = 34 cm2
Anm.: En alternativ lösning är att beräkna den lilla kvadratens sida med Pytagoras sats...

Rektanglarna
Svar:
100 cm
Lösning:
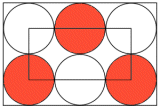
Den lilla rektangelns omkrets är sex gånger så stor som diametern i en cirkel. Cirkelns diameter är då 60 cm/6 = 10 cm.
Den stora rektangelns omkrets är tio gånger så stor som diametern i en cirkel.  10 . 10 cm = 100 cm
 

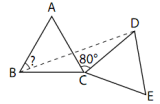
Trianglarna
Svar:
40o
Lösning:
Triangeln BCD är likbent, och vinkeln BCD är (60 + 80)o = 140o
Då är vinkeln CBD = (180 - 140)/2 = 20o
Då är vinkeln ABD = 60o - 20o = 40o

Lajka
Svar:
72 m
Lösning:
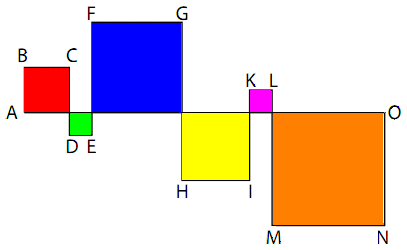
Summan av en sida från varje kvadrat är 24 m.
Lajka springer utmed tre sidor i varje kvadrat. 3 . 24 m = 72 m


Madame Dupont

Svar: 8 km
 Lösning:
Antag att den plana sträckan är a km och backen b km.
Den sammanlagda tiden ger följande ekvation:
2a/4 + b/3 + b/6 = 2
Efter förenkling får man  a + b = 4   
Madame Dupont sammanlagda sträcka är 2a + 2b
                               2a + 2b = 8


Gula området

Svar: 2 cm2
 Lösning:
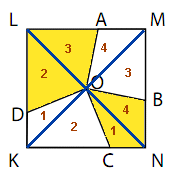
Genom att utnyttja att vinklarna AOB och COD är räta samt att vinkelsumman i en triangel är 180o , kan man visa att trianglarna parvis är kongruenta (1-1, 2-2 osv.)
Arean av kvadraten KLMN är 2 . 2 cm2  = 4 cm2
Det gula området är hälften så stort, dvs. 2 cm2.


Kvadraterna del 2

Svar: 1 cm2
 Lösning:
Flytta triangeln DEH till triangeln CFG och triangeln BEF till triangeln CGH.
Då täcker det ursprungligen gula området precis kvadraten  EFGH.

Enligt uppgiften är det gula området 1 cm2.
Kvadraten ABCD är därför 1 cm2
 
   

|Tillbaka|