Klurigt nr 18 (lösningar)
 
"Rävgiftet"
Svar: Lika mycket
Lösning:
Eftersom koppen först var fylld med enbart kaffe, måste moster Agda ha druckit en hel kopp kaffe.
Hon fyllde koppen i tre omgångar med mjölk på följande sätt:
En sjättedel, en tredjedel resp. hälften av koppens volym.
Men 1/6 + 1/3 + 1/2 = 1. Alltså drack Agda också en hel kopp mjölk.
 

Använd bara sunt förnuft!
Svar:
Båda skeppen befinner sig 1250 m från skärningspunkten.
Med Pytagoras sats kan man beräkna att avståndet mellan skeppen är

Lösning:
Det verkar inte rimligt att något skepp skulle vara längre från skärningspunkten än det andra skeppet, när avståndet mellan dem är som kortast.

Vi antar skeppen är olika långt från skärningspunkten, när avståndet är som kortast, och visar att detta är orimligt.

Antag att avståndet från skärningspunkten är (1250 + a) m resp. (1250 - a) m.
Avståndet (x) mellan skeppen beräknas med Pytagoras sats:
x =
För att avståndet x skall vara så litet som möjligt måste a = 0.
De båda skeppen befinner sig alltså lika långt från skärningspunkten, dvs. 1250 m.
Avståndet mellan skeppen är m.
 

Ombytta roller
Påst.: ab . cd = ba . dc

Bevis:
Värdet av talet ab är i vårt tiotalssystem 10 . a + b

Sambandet kan därför skrivas (10 . a + b)(10 . c + d) = (10 . b + a)(10 . d + c)
Vi förenklar ovanstående uttryck
100ac + 10ad + 10bc + bd = 100bd + 10bc +10ad + ac
                            99 ac = 99 bd
                                ac  = bd

I ord kan det uttryckas så här:
Villkoret är att produkten av faktorernas tiotalssiffror ska vara lika stor som produkten av faktorernas entalssiffror.

Ex.: 23 . 64 = 32 . 46
      2 . 6 = 12
      3 . 4 = 12

Ytterligare ett exempel: 93 . 26 = 39 . 62
Alfametik

Ta ett tal
Svar: T = 2   A = 5   E = 1   L = 3

    2 5
  1 2 2
+ 2 5 3
  4 0 0

Ledning:
Det framgår av hundratalssiffrorna, att man måste undersöka två alternativ:
1) T = 1 och E = 2
2) T = 2 och E = 1
Det första alternativet duger inte eftersom E och L då båda får värdet 2.

Den lille trollkarlen
Svar: 35985 (kr)

  A=5   B=9   D=3   K=7   R=8

  5 9 8 5
  5 9 8 5
  5 9 8 5
  5 9 8 5
  5 9 8 5
  5 9 8 5
+     7 5
3 5 9 8 5

Lösningen kan kontrolleras på http://www.iread.it/cryptarithms.php i spalten Solve

Fartsyndaren
Svar: 2515 (kr)

A=5  F=2  O=0  R=1  T=3

    2 5 1
    2 5 1
+ 2 0 1 3
  2 5 1 5

Lösningen kan kontrolleras på http://www.iread.it/cryptarithms.php i spalten Solve
 
Ett problem som kan lösas enkelt med lite fantasi!
Svar: Hälften av kvadraten är målad
Lösning: Flytta de gula områdena till platsen för de blå områdena!

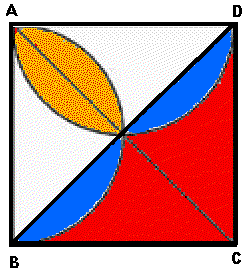
Anm.: Gemensamt för de fyra sista geometriska uppgifterna är att det med lite fantasi går att hitta enkla lösningar!

Rektanglarna
Svar: 12 cm2
Lösning:
Arean av triangeln ABD 6 cm2. Då är arean av triangeln DBC också 6 cm2.
Men arean av triangeln DBC är hälften av arean av rektangeln DBEF.
Alltså är arean av rektangeln DBEF 2 . 6 cm2 = 12 cm2

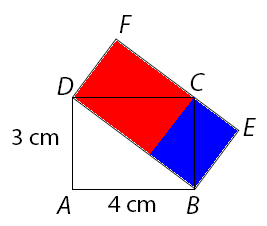Hexagonen
Svar: 16 cm
Lösning:


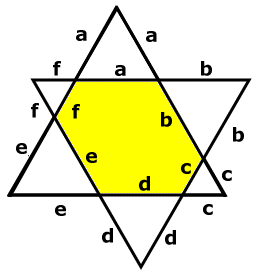
Med fig. beteckningar blir de ursprungliga liksidiga trianglarnas sammanlagda omkrets
3(a+b+c+d+e+f) = 48
    a+b+c+d+e+f = 16

Men a+b+c+d+e+f är ju omkretsen av hexagonen. Alltså har vi löst problemet!
 
Ett bra förhållande?
Svar: Sträckorna AE och ED förhåller sig som 3:1
Lösning:

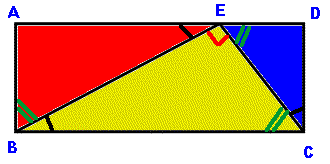
Av vinkelbeteckningarna framgår att triangeln BCE är rätvinklig och dessutom likformig med de båda andra trianglarna.

 Vi vet att CE:BC = 1:2, dvs. den minsta kateten är hälften av hypotenusan i triangeln BCE.

Antag att BC = AD = 4x (l.e.). Då är CE = 2x (l.e.)

Betrakta nu triangeln CDE.
Även här är den minsta kateten hälften av hypotenusan, eftersom alla tre trianglarna är likformiga.
Då är längden av DE hälften av längden av sträckan CE.
DE = 2x/2 = x (l.e.)
Enligt vårt antagande är AD = 4x (l.e.).
Därför är AE = 4x – x = 3x (l.e.)

Förhållandet mellan sträckorna AE och ED är 3x/x = 3:1
 
 


|Tillbaka |