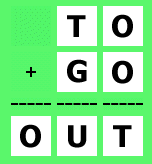Klurigt nr 18

Klurigt nr 18

Det mystiska talet sju
Världens sju nya underverk röstades fram 070707:
Chichén Itzá i Mexico, Colosseum i Rom , Kristusstatyn i Rio de Janeiro, Machu Picchu i Peru, Kinesiska muren, Petra i Jordanien och Taj Mahal i Indien.
Mer info finns på Wikipedia

Rekordmånga gifte sig just 070707.

Vad är det för speciellt med talet 7?

Läs mer

Wikipedia (svensk version)
Illustrerad Vetenskap

Wikipedia (engelsk version)
The Number Seven

Talmystik (Numerologi)

Universums talmystik (bl.a. astrologi; vissa felaktigheter förekommer)

"Rävgiftet"

En dag råkade moster Agda av misstag koka alldeles för starkt kaffe. Hon hällde upp en full kopp kaffe och drack upp en sjättedel av innehållet.
- Usch då! Rena rävgiftet sa Agda och fyllde koppen med mjölk.
Hon drack upp en tredjedel av drycken.
- Fortfarande för starkt, muttrade Agda.
Hon fyllde än en gång på med mjölk så att koppen blev full.
Därefter drack hon ur hälften av drycken.
- Fortfarande för magstarkt, sa Olga och fyllde koppen med mjölk.
- Äntligen drickbart, sa Olga, och med några rejäla klunkar svalde hon all dryck i koppen.
Hade moster Agda druckit mest kaffe eller mjölk?

Använd bara sunt förnuft!

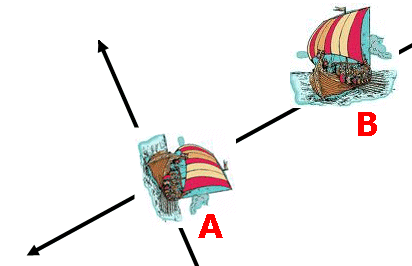
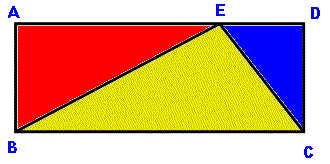
Två vikingaskepps kursriktning bildar 90º vinkel med varandra. De seglar lika fort. När skepp A är i skärningspunkten för skeppens kursriktningar, har skepp B 2500 m kvar till skärningspunkten.
Var befinner sig skeppen i det ögonblick, som de är närmast varandra?

Anm.: Det här problemet går att lösa genom t.ex. derivering, men egentligen behövs det inte några speciella matematikkunskaper. Det går att resonera sig fram till en lösning med lite sunt förnuft:
I utgångsläget är avståndet mellan skeppen 2500 m.
När skepp B har kommit till skärningspunkten, är avståndet också 2500 m.
Någon gång mellan dessa tidpunkter har vi det kortaste avståndet mellan skeppen.
På vilket avstånd från skärningspunkten bör detta inträffa?

Ombytta roller!

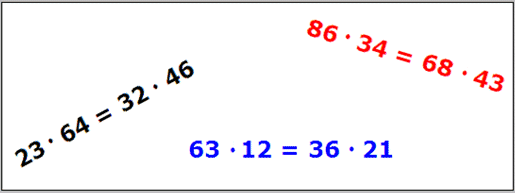
I de här exemplen gäller likheterna, fastän tiotals- och entalssiffran bytt plats i det högra ledet jämfört det vänstra ledet.

Man kan lätt konstatera att detta samband inte gäller för alla tvåsiffriga tal.

Uppg.: Ange det villkor, som ovanstående exempel uppfyller,
dvs. att ab ^.cd = ba ^.dc

Alfametik

I en alfametik skall varje bokstav ersättas av en siffra.
Olika bokstäver betyder olika siffror. Dessutom får inget tal börja med siffran noll.
Bokstäverna skall också bilda meningsfulla ord eller fraser.

Historik med exempel Tre nya originalproblem

Exempel som kan lösas direkt på webben!

Ett problem som kan lösas enkelt med lite fantasi!

Hur stor del av kvadratens area är målad med röd färg?

Rektanglarna
I fig. till höger finns det två rektanglar,
ABCD och DBEF.
Hur stor är arean av rektangeln DBEF?

Hexagonen
Två liksidiga trianglar, som var och en har omkretsen 24 cm, är placerade ovanpå varandra med respektive sidor parallella som fig. till höger visar.
Hur stor omkrets har den gula sexhörningen
(hexagonen)?

Ett bra förhållande?
Trianglarna ABE och CDE är likformiga.
Sträckorna CE och BC förhåller sig som 1:2.
Vilket är förhållandet mellan sträckorna AE och ED?

|Tillbaka till Klurigt|Lösningar|

Alfametik

Historik

Ett klassiskt exempel av H. E. Dudeney publicerades 1924:

	S	E	N	D		9	5	6	7
+	M	O	R	E	+	1	0	8	5
M	O	N	E	Y	1	0	6	5	2

Bakgrunden till problemet skulle kunna se ut så här:
En fattig student telegraferar till sin far och ber om mer pengar.
Han anger inget belopp, men fadern inser, att hans intelligente
son har dolt beloppet i detta krypto.

Andra välkända exempel är

	H	A	U	S		6	4	1
+	H	A	U	S	+	6	4	1
S	T	A	D	T	1	2	8	2


	C	R	O	S	S		9	6	2	3	3
+	R	O	A	D	S	+	6	2	5	1	3
D	A	N	G	E	R	1	5	8	7	4	6

År 1969 publicerade Steven Kahan den första s.k. dubbelt sanna
alfametiken, där additionen också stämmer om orden ersätts med tal.

Exempel på dubbelt sanna alfametiker:

	E	T	T		1	2	2
	E	T	T		1	2	2
	E	T	T		1	2	2
	E	T	T		1	2	2
+	E	T	T	+	1	2	2
	F	E	M		6	1	0

			O	N	E				3	9	1
			T	W	O				8	0	3
			T	W	O				8	0	3
	T	H	R	E	E		8	4	6	1	1
+	T	H	R	E	E		8	4	6	1	1
E	L	E	V	E	N	1	7	1	2	1	9

Ett enkelt exempel

	Hundratalssiffran i svaret har kommit från en minnessiffra. När två tal adderas, är ett den enda tänkbara minnessiffran. O = 1
	T = 2
	För att det ska bli en minnessiffra i hundratalskolumnen, måste G vara lika med åtta eller nio, men nio duger inte, eftersom U i så fall skulle bli 1 (O = 1). G = 8
	U = 0

Tillbaka

Tre nya originalproblem

Ta ett tal

Ta ett tal! sa professor Kalkyl till en av sina elever.
400, sa eleven.
Märkligt! utropade professor Kalkyl.
Titta på den här algoritmen:

		T	A
	E	T	T
+	T	A	L
	4	0	0

Varje bokstav kan ersättas av en siffra så att additionen stämmer.
Olika bokstäver betyder olika siffror. Dessutom får inget tal börja med siffran noll.
Visa nu vilka tal, som har adderats.

Tillbaka

Den lille trollkarlen.
- Abrakadabra, sa den lille trollkarlen. Nu ska jag trolla fram jättemycket pengar.
- Den där gamla trollformeln duger inte längre, sa hans läromästare.
Istället ska du säga så här:
Abra, abra, abra, abra, abra, abra, kadabra!
- Oj, oj, oj vad mycket pengar du trollade fram! Hur mycket är det egentligen? frågade den lille trollkarlen.
- Räkna ut den här additionen, så har du svaret.

+			K	A
	A	B	R	A
	A	B	R	A
	A	B	R	A
	A	B	R	A
	A	B	R	A
	A	B	R	A
D	A	B	R	A

Varje bokstav ska ersättas av en siffra.
Olika bokstäver betyder olika siffror. Dessutom får inget tal börja med siffran noll.

Tillbaka

Fartsyndaren
- Pappa, du kör alldeles för fort!
Jag slår vad, att du åker fast för fortkörning inom en månad.
- Hur mycket ska vi slå vad om?
- Den här additionen ger dig svaret!

		F	A	R
		F	A	R
+	F	O	R	T
	F	A	R	A

Varje bokstav ska ersättas av en siffra.
Olika bokstäver betyder olika siffror. Dessutom får inget tal börja med siffran noll.
Anm.: Frasen "FAR FAR FORT = FARA" är en alliteration!

Tillbaka

Ett problem som kan lösas enkelt med lite fantasi! Hur stor del av kvadratens area är målad med röd färg?
Rektanglarna I fig. till höger finns det två rektanglar, ABCD och DBEF. Hur stor är arean av rektangeln DBEF?
Hexagonen Två liksidiga trianglar, som var och en har omkretsen 24 cm, är placerade ovanpå varandra med respektive sidor parallella som fig. till höger visar. Hur stor omkrets har den gula sexhörningen (hexagonen)?