Klurigt nr 16 (lösningar)

Palindrom  

Uppgift: Utnyttja talen 2, 2, 3, 7, 13 och 37 för att bilda en palindrom. Ex.:  1) 37 - 13 - 2 . 7 + 3 - 2 = 11 2)  37 . (13 - 2 . 2 . 3) + 7 = 44 3) 4)  37 + 13 + 7 -3 + 2/2 = 55 5)  2 . 7 + 3 . 13 + 37 - 2 = 88 6) 3 . 37 + 7 . 13 . (2-2) = 111 7) (2+2)3 + 7 + 13 + 37 = 121 8) 9)

Räknegåtan

Svar:  Talet är 36 eller 75. Lösning: Antag att talet är x   (0<x<100) Påst.: (10x - 9)/39 ger ett heltalssvar (a). Eftersom sista siffran i täljaren (10x-9) är en etta, måste  sista siffra i kvoten (a) vara en nia. Det räcker därför att undersöka a= 9, 19 och 29. Bevis:  a = 9  x = (39 . 9 + 9)/10 = 36 a = 19 x = (39 . 19 + 9)/10 = 75 (a = 29 x = (39 . 29 + 9)/10 = 114)

 Räknetricket

Svar:  a) Man får reda på det mellersta av de tre talen. b) Gör ett symmetriskt antagande, dvs. kalla talen x-2, x och x+2 Bevis: Summan: x-2+x+x+2 = 3x Summan upphöjt till 3: (3x)3 = 27x3  Division med 27: 27x3 / 27 = x3 Division med x2: x3/x2 = x (dvs. det mellersta talet enligt antagandet)  OBS! x ≠ 0 c) Det mellersta talet får inte vara 0. Om det mellersta talet är 0, bryter man mot det elfte budet: "Du skall icke dividera med noll!"

Produktkontroll

Svar:  Alt. 1: På Annas lappar finns talen 2, 3 och 8 och  på Emmas  1, 5 och 6. Alt. 2: På Annas lappar finns talen 1, 6 och 8 och  på Emmas  2, 3 och 5. Lösning: Produkten av Annas tal är 48. Det ger följande tre möjligheter: 1) 1 . 6 . 8 2) 2 . 3 . 8 3) 2 . 4 . 6 Produkten av Emmas tal är 30. Det finns två tänkbara möjligheter: 1) 1 . 5 . 6 2) 2 . 3 . 5 Med alternativet 1 . 5 . 6 (Emmas lappar) kan Anna endast ha talen 2, 3 och 8. Med alternativet 2 . 3 . 5 (Emmas lappar) kan Anna endast ha talen 1, 6 och 8. Anm.: Emma och Anna kan lista ut vilka lappar den andra har, men som problemlösare har du inte den möjligheten.

Magister Rask

Svar: Talet är 1201 Lösning: Eftersom magister Rasks tal ökade med 6060, när eleverna skrev sitt tal, måste det ha varit tusentalssiffran och tiotalssiffran, som var slarvigt skrivna. Ett fyrsiffrigt heltal kan inte ha en nolla som tusentalssiffra. Därför vet vi hur vi ska placera ettan och nollan: 1 o 0 o  Ledtråd 1: Siffersumman är 4. Det ger oss följande möjligheter: 1003 1300 1102 1201 Ledtråd 2: Talet är ett primtal. Men ett primtal (>2) är alltid ett udda tal! Därför behöver vi bara undersöka talen 1003 och 1201. 1003: 1003/17 = 59. Talet 1003 är inget primtal och är därför inte det sökta talet. Då återstår bara talet 1201, som vid en kontroll visar sig vara ett primtal!

En smart lösning
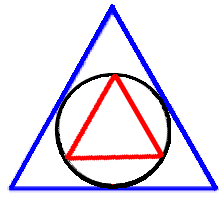
Svar: Trianglarnas areor förhåller sig som 4:1. Om man vrider den röda liksidiga triangeln 180o, inser man lätt att arean av den blå triangeln är fyra gånger så stor som den röda triangelns area.

Ytterligare ett exempel: Hur stor är den blå kvadratens area jämfört med den röda kvadratens area i fig. nedan till vänster? Svar: Genom att vrida den röda kvadraten 45o (fig. nedan till höger) inser man lätt att den blå kvadraten har dubbelt så stor area som den röda kvadraten.

Hunden och soldaterna

Svar: Hunden springer sammanlagt 90 m. Lösning: Eftersom hundens fart är tre gånger så hög som soldaternas, måste soldaterna ha gått en sträcka som är en tredjedel av vad hunden har sprungit, när han når fram till den första soldaten. Avståndet från den sista till den första soldaten (40 m) motsvarar alltså 2/3 av hela sträckan för hunden, dvs. hunden har sprungit 60 m. När hunden vänder tillbaka kommer han att springa 3/4 av avståndet från den första till den sista soldaten (40 m), dvs.  30 m. (Hundens fart är 3/4 av hundens och soldaternas sammanlagda fart.) Totalt: 60 m + 30 m = 90 m Problemet kan också lösas med ekvation. Det finns flera varianter. En av dem ser ut så här: Antag, att soldaternas fart är v m/s och hundens fart 3v m/s. Fall 1: Antag att hunden springer a m i samma riktning som soldaterna Ekv.: a/3v = (a-40)/v      a = 60 m  Fall 2: Antag att hunden springer b m i motsatt riktning Ekv.: b/3v = (40 - b)/v            b = 30 m Totalt: 60 m + 30 m = 90 m

Perifert men inte oväsentligt!
Svar: Vinkeln v (fig. 1) är 135o Lösning: Medelpunktsvinkeln u till den gröna bågen (fig. 2) är 270o. Vinkeln v är periferivinkel (randvinkel) på samma båge och enligt randvinkelsatsen hälften så stor.
fig. 1	fig. 2

Apan och kokosnötterna

Svar: a)  Om apan fick n nötter fanns det från början 2n+1 -2  nötter. Lösning:  Om apan fick 1 nöt, fanns det 2 nötter från början. Om apan fick 2 nötter fanns det 6 nötter från början. Om apan fick 3 nötter fanns det 14 nötter från början osv. Formeln 2n+1 -2 för totala antalet nötter passar in på de här exemplen. Ex.: n = 3 2n+1 -2 = 23+1 - 2 = 24 - 2 = 16 - 2 = 14 Man kan också beskriva lösningen med en s.k. rekursionsformel: an+1 = 2(an +1)        a1 = 2 (nötter), dvs. om apan fick n nötter var an totala antalet nötter  Utveckling av rekursionsformeln ger an = 2n + 2n-1 + ..... + 2 = 2n+1 - 2 b) Apan får 9 nötter. Lösning: 2n+1 - 2 = 1022 2n+1 = 1024 2n = 512 n = 9

Skattkartan

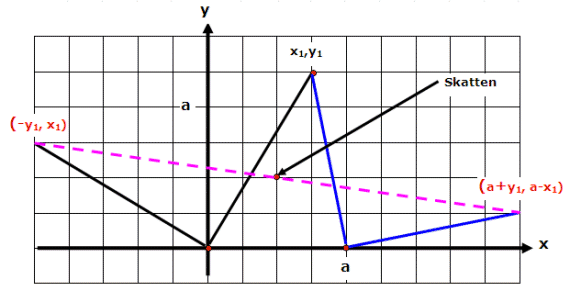Lägg in palmerna och galgen i ett koordinatsystem och antag att palmerna har koordinaterna (0,0) och (a,0), medan galgen har kooordinaterna (x1,y1). Då hamnar käpparna på (-y1, x1) och (a+y1,a-x1). Mittpunkten blir då 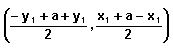dvs. . Därför kan jag lösa problemet utan att känna till galgens placering: Jag letar upp mittpunkten mellan palmerna och ställer mig så att jag har den västra palmen till vänster. Sedan går jag - vinkelrätt mot förbindelselinjen mellan palmerna - en sträcka som motsvarar halva avståndet mellan palmerna. Anm.: Beviset gäller generellt, dvs. även om  x1<0 eller om x1>a.

För denna sida ansvarar: Alf Gunnarsson

|Tillbaka |