Klurigt nr 15 (lösningar)

Fältteori 

Svar: Hälften Lösning: Triangeln ACF:s area är hälften så stor som triangeln ACD:s area (AD är höjd i båda trianglarna). Triangeln AEC:s area är hälften så stor som triangeln ABC:s area (AB är höjd i båda trianglarna).

Olyckstalet? 

Lösningen kan se ut så här (fig. till höger) Komm.: Summan av de åtta talen är 36 och summan längs alla fyra sidorna är 52. Det betyder att summan av de fyra talen i hörnen måste vara 16. (52 - 36 = 16)

Motionsrundan

Svar: 25% Lösning: s = v . t Ekv.: 4 . x. t = 3 . t   (x = förändringsfaktorn för tiden)      x = 0,75  Förändringsfaktorn = 0,75 = 75% dvs. sänkningen är 25%

Fotbollsserien

Svar:  a) 90 matcher spelades b) Serien bestod av 10 lag Lösning:  Problemen kan lösas med ekvation, men det går också bra med följande resonemang: a) Andelen vunna matcher ökar från 1/2 till 2/3, dvs. med 1/6. Totala poängskörden ökar med 15 p. När en oavgjord match ändras till en vunnen match utdelas tre poäng istället för två poäng: 15 matcher som slutade med oavgjort resultat ska alltså ändras till vinstmatcher.  15 matcher är således 1/6 av matcherna. Totala antalet matcher är därför 6 . 15 = 90 b) Antalet matcher = (antalet lag) . (antalet lag - 1) 90 = 10 . 9

Förhållandet

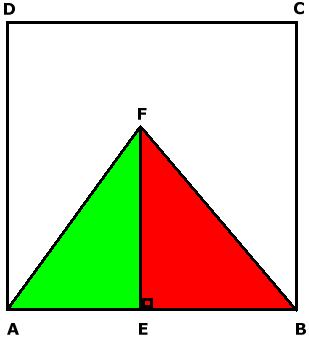
Svar: 2:3 Lösning: Triangeln ABF:s area är 40% av kvadratens area. Då är höjden EF 4 cm (80% av kvadratens sida). Enligt Pytagoras sats blir då EB = 3 cm, vilket medför att AE =2 cm. Eftersom trianglarna AEF och BFE har samma höjd förhåller sig areorna som baserna AE och EB, dvs. 2:3.

Spelkorten

Svar: Alexander: Två kungar och två damer. Benny: Fyra knektar. Crille: Tre ess och en kung. David: Ett ess, en kung och två damer. Lösning (alt. 1) Alexander: Poängvärdet 50 ger följande alternativ 11  11  14  14               11  12  13  14               11  13  13  13               12  12  12  14 12  12  13  13         Benny: Enda alternativet är fyra knektar. Det betyder att Alexanders tre första alternativ är otänkbara. Crille: Enda alternativet är tre ess och en kung.  David: Poängvärdet är 51. Det ger följande alternativ 11  12  14  14               11  13  13  14               12  12  13  14               12  13  13  13                De två första alternativen med knektar är otänkbara. Davids första kort är ett ess, dvs. det tredje alternativet är det rätta. Det betyder att Alexanders fjärde alternativ är det enda som passar. P.S. Följande BASIC-program ger antalet alternativ för resp. poängvärde:  10 FOR A=11 TO 14 20 FOR B=11 TO 14 30 IF B<A THEN 140 40 FOR C=11 TO 14 50 IF C<A THEN 130 60 IF C<B THEN 130 70 FOR D=11 TO 14 80 IF D<A THEN 120 90 IF D<B THEN 120 100 IF D<C THEN 120 110 IF A+B+C+D=50 THEN PRINT A;B;C;D,:REM GER ALTERNATIVEN FÖR POÄNGVÄRDET 50 120 NEXT D 130 NEXT C 140 NEXT B 150 NEXT A Lösning (alt. 2 - en snabbare lösning): Benny: Poängvärde: 44. Enda alternativet är fyra knektar.   Crille: Poängvärde: 55. Enda alternativet är tre ess och en kung.  David: Ett ess. Alexander: Poängvärde: 50. Eftersom han inte kan ha något ess, måste han ha två kungar och två damer. David: För David återstår nu följande kort: ett ess, en kung och två damer. Poängvärde: 51

Tre tal

Svar: 7, 5 och 3 eller 9, 6 och 5 Ett enkelt BASIC-program ger svaret: 10 FOR X=1 TO 9 20 FOR Y=1 TO 9 30 IF Y=X THEN 90 40 FOR Z=1 TO 9 50 IF Z=X THEN 80 60 IF Z=Y THEN 80 70 IF X+Y+Z=X^2-Y^2-Z^2 THEN PRINT X;Y;Z, 80 NEXT Z 90 NEXT Y 100 NEXT X

Urfånigt!?

Svar: Det finns två lösningar:  kl. 03.20 (15.20) och 08.40 (20.40) Lösning: Minutvisaren rör sig 6o per min och timvisaren 0,5o per min, dvs. 30o på en timme. Fall 1: Minutvisaren har passerat timvisaren när vinkeln 20o bildas. Antag att 1) vinkeln 20o bildas efter x min (räknat från när klockan visade hel timma senast) 2) senaste heltimmen var kl. a Ekv.: 6x - (30a + 0,5x) = 20     dvs. x= 20(3a+2)/11 Endast a=3 ger en heltalslösning för x   (x=20) Fall 2: Minutvisaren har inte passerat timvisaren när vinkeln 20o bildas. Samma antagande som i fall 1. Ekv: 30a + 0,5x - 6x = 20     dvs. x= 20(3a-2)/11 Endast a=8 ger en heltalslösning för x   (x=40) OBS! Lösningarna kan skrivas Det innebär att lösningarna ligger symmetriskt: 3h 20 min före resp. efter kl. 12.

Tangenterna

Svar:  a) Triangelns omkrets: 40 cm   b) Triangelns area: 60 cm2   c) Cirkelns radie: 12 cm Lösning: a) Utnyttja att tangenter från samma punkt är lika långa. AC = AB = 20 cm, FC = FE och DB = DE. Därför är triangelns omkrets lika lång som summan av tangenterna AB och AC. b) Antag att EF = x cm och DE = 4x cm Då är AF = (20 - x) cm och AD = (20 - 4x) cm, eftersom FC = FE och DB = DE. Pytagoras sats på triangeln ADF ger (20-4x)2 + (5x)2 = (20-x)2 (x1 = 0)   x2 = 3    DF = 5x = 5 . 3 = 15     AD = 20 - 4x = 20 - 4.3 = 8 Arean är 8.15 cm2/2 = 60 cm2. c) Radien OB är lika lång som sträckan DE, dvs. 12 cm.

Parkeringsplatsen 

Svar: Kvastarna kunde byta plats på 44 sätt. Generell lösning: Uppgift: n st kvastar placerade på n st parkeringsplaser skall placeras om så att ingen kvast finns kvar på sin ursprungliga plats. På hur många olika sätt kan detta göras? Svar: En formel för att beräkna antalet sätt kan skrivas så här: n! (n!/2! - n!/3! + n!/4!... + (-1)n . n!/n!) Specialfallet n = 5 n=5 ger 5!(1/2! - 1/3! + 1/4! - 1/5!) = 120(1/2 - 1/6 + 1/24 -1/120)=60 - 20 +5 -1 = 44

 

För denna sida ansvarar: Alf Gunnarsson

|Tillbaka |