Kub I

Svar: 20 kuber  (27-6-1=20)

Kub II

Svar: 14 röda kuber

Temaarbetet

Svar: 5400 cm2, dvs. ca 0,5 m2. De kvadratiska teckningarna har vardera sidan 360 cm/4 = 90 cm. Den stora kvadratens sida är därför 180 cm. Längden av en rektangulär teckning är 90 cm och bredden är 180 cm/3 = 60 cm. Arean är därför 90 Ÿ 60 cm2 = 5400 cm2.

Mobiltelefonerna

Svar:  a) 1/6   b) 2/3  (Beräkna komplementhändelsen, dvs att ingen får tillbaka sin telefon: 2/3 * 1/2 = 1/3      1 - 1/3 = 2/3) c) Denna händelse kan inte inträffa!  Om två får tillbaka sina telefoner, får också den tredje tillbaka sin telefon.

Besöket på puben

Svar: Peter kan inte vara belåten!  Sannolikheten att Peter får betala är 50%, eftersom det finns fyra utfall (krona, krona   krona, klave   klave, krona    klave, klave)

Pinnarna

Svar: Sannolikheten att pinnen har samma färg i båda ändarna är 2/3. Ex.: Antag att den ända som visas är svart. Det finns då tre möjligheter (Se figur). I två av dessa fall är den andra änden svart.

Kulorna

Svar: Från början finns det 14 röda och 12 blå kulor i påsen. Lösning: Första kulan röd: 48% av de återstående är blå. Första kulan blå: 56% av de återstående är röda, dvs. 44% är blå. 48%-44%=4%, dvs. en kula motsvarar 4% av antalet kulor efter första dragningen. Antalet kulor är då 25 st. Från början finns det 26 kulor, 14 röda (=56/4) och 12 blå (=48/4).

Saab 99 Turbo

Svar: Claes-Göran kunde köra 5400 mil. Lösning: För varje mil slits alla fyra däcken sammanlagt 2/3600 + 2/5400, dvs. sammanlagt 5/5400. Om slitaget fördelas jämnt på de fem däcken, kan man köra med dem 5/(5/5400) mil = 5400 mil Anm.: Är det här problemet realistiskt? Knappast. Lösningen förutsätter att reservdäcket används både på vänstra och högra sidan. Men då byter man rotationsriktning, och det är ju inte lämpligt.

De nio siffrorna

Svar: Om villkoret i uppgiften skall uppfyllas, måste siffersumman i svaret vara 18. Ex: 182 + 394 = 576 Lösning:1 + 2 + 3 + ..... + 9 = 45 Låt siffrorna i det första talet vara a, b och c. Det andra talets siffror är d, e och f. Siffrorna i talens summa är g, h och i. Undersök om det kan förekomma några minnessiffror! Alt. 1: Ingen minnessiffra Då gäller att a + b + c + d + e + f + g + h + i = 45     och a + b + c + d + e + f = g + h + i dvs. g + h + i = 22,5 vilket är orimligt! Alt. 2: En minnessiffra Då gäller att  a + b + c + d + e + f + g + h + i = 45     och a + b + c + d + e + f = g + h + i + 9 (minnessiffran räknas som 1 stället för 10 i siffersumman: 10 - 1 = 9) dvs. g + h + i = 18 Alt. 3: Två minnessiffror Då gäller att  a + b + c + d + e + f + g + h + i = 45     och a + b + c + d + e + f = g + h + i + 9 + 9 dvs. g + h + i = 13,5 vilket är orimligt! Slutsats: Om villkoret i uppgiften skall uppfyllas, måste siffersumman i svaret alltid vara 18. Anm.: Det finns 168 unika kombinationer. Då har jag räknat t.ex. 124+659=783 och 659+124=783 som en kombination.

Agdas bröder

Svar: Den yngste brodern är född 1950-10-02. De två äldre bröderna är tvillingar, födda 1941. Lösning: 173 = 4913  183 =5832  193 =6859. Enda tänkbara summan av brödernas födelseår är 5832. I snitt ger det födelseåret 1944. Den yngste brodern är därför född senare än 1944.  w Eftersom alla födelseåren har samma siffersumma, måste ålderskillnaden mellan bröderna vara n*9, där n= 0,1,2,3... w För att få en geometrisk serie, som passar för år, månad och dag undersöker vi om kvoten mellan två termer kan vara 1/6, 1/5 eller 1/4. (Inga andra kvoter är tänkbara.) 1/6: Endast årtalet 1972 är lönt att testa. De sex första siffrorna skulle kunna vara 721202, men inga födelseår för bröderna uppfyller villkoret att summan av födelseåren skall vara 5832. 1/5: Endast årtalet 1950 är lönt att testa. Här hittar vi en lösning: De sex första siffrorna är 501002. De äldre bröderna är tvillingbröder och födda 1941, vilket ger 5832 som summa av födelseåren. 1/4: Endast årtalet 1948 är lönt att testa. 1948: De sex första siffrorna skulle kunna vara 481203, men inga födelseår för bröderna uppfyller villkoret att summan av födelseåren skall vara 5832.

Ljusstaken

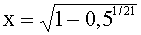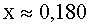
Svar:  a) Den procentuella förändringen av tiden är 18,0 %. Lösning: Sex färger och sju lampor : 42 är det minsta tal som är jämnt delbart med 6 och 7. När lampa  nr 1 lyser med rött sken andra gången, har lystiden ökat resp. minskat 21 gånger. Antag att förändringsfaktorerna för ökning resp. minskning av tiden är (1+ x) och (1 - x). Ekv.: 10,0 *(1+x)21 *(1-x)21 = 5,0           b) Lampa nr 1 har visat rött sken fyra gånger, innan den återgår till att visa rött sken under 10,0 s. Lösning:  Antag, att ökning och minskning av lystiden har skett n gånger, när lystiden (utan korrigering) skulle bli mindre än 1 s. 10,0 *(1,18)n *(0,82)n <1,0  n > 69,9 Lampa nr 1 lyser röd för följande x-värden: x = 0 x = 21 x= 42 x = 63 För x = 84 måste datastyrningen ställa om tiden till 10,0 s.