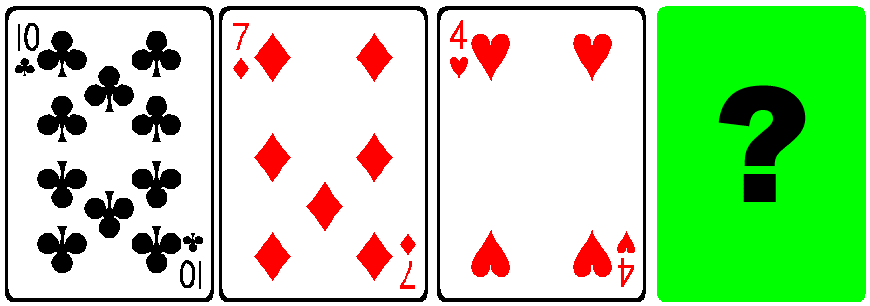
Vilket är det dolda kortet?
Klurigt nr 13
Det dolda kortet
 Vilket är det dolda kortet? |
Kvadraterna
| Hur många kvadrater finns det i fig. till höger? |  |
Fåglarna
| Anna,
Benny och Cilla hade förra veckan ett läxprov i biologi, som handlade om
"Skogens fåglar". Bl.a. skulle de känna igen de fyra fåglar
som finns avbildade här (men som inte är placerade i rätt ordning). Så här svarade de: Anna: "Trean är talgoxe och fyran är en bofink. Benny: "Ettan är en bofink och trean en talgoxe. Cilla: "Tvåan är en blåmes och fyran en rödhake. Varje elev hade ett riktigt och ett felaktigt svar. Kan du bestämma i vilken ordning fåglarna kommer? |
|
|
|
|
|
 |
En ny räkneregel
| I landet
Multavien får eleverna lära sig en räkneregel, som betecknas med Ex: 3
|
Trianglarna
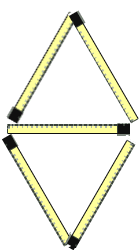
| I figuren till
höger har man lagt fem stickor så att de bildar två liksidiga
trianglar. Hur ska man kunna bilda fyra lika stora och liksidiga trianglar med hjälp av endast sex stickor? |
 |
Biljardbollarna I
| I en låda ligger 27 biljardbollar. Alla ser likadana ut, men en av bollarna väger mer än de andra. Går det att med hjälp av enbart en balansvåg (utan några vikter) hitta den felaktiga bollen på bara tre vägningar? |  |
Trollen
| Trollen Klumpeduns
och Vresig spelar om tio guldmynt, som ligger i två högar. Så
här går det till: I varje drag får en spelare ta bort ett mynt från någon av högarna eller ett mynt från vardera högen. Den som tar bort det sista myntet vinner alla tio guldmynten! Trollen drar lott om vem som skall börja. Klumpeduns vinner lottdragningen. Han kan då välja att börja själv, men han kan också överlåta åt Vresig att göra första draget. Hur tycker du att Klumpeduns ska göra? Finns det någon vinnande strategi? |
Korttricket
| Imponera som
tankeläsare på din bekantskapskrets ! Utförande: Korten i en vanlig kortlek skall läggas i högar enligt följande regel: Vänd hela kortleken så att det första kortets valör är synlig (fig. 1). Räkna kort från första kortets valör (ess räknas som 1) upp till 13 och låt dessa kort bilda en hög, som läggs så att det sista kortets valör blir synlig . Börja sedan på en ny hög genom att utgå från valören på det kort som nu är synligt i kortleken. Ex.: Om kortets valör är 10 (fig. 1), räknar man 10, 11, 12, 13, dvs. 10:an och ytterligare tre kort från kortleken kommer att bilda en hög, så att det sist tagna kortet är synligt (fig. 2). När man lagt ut så många kort som möjligt - några kort går förmodligen inte att lägga ut - vänder man på tre av högarna. Vi kan kalla dem för hög 1, 2 och 3. Övriga kort, dvs. återstående högar och ev. överblivna kort läggs åt sidan i en särskild hög, som vi kallar för hög S (=slask) Från hög S tar man sedan kort på följande sätt: a) Först tar man bort 10 kort. b) Sedan vänder man på det översta kortet i hög 1 och tar bort lika många kort från hög S som valören för det kort som nu syns i hög 1. c) Sedan vänder man det översta kortet i hög 2 och tillämpar samma metod. Därefter påstår man att antalet kort, som finns kvar i hög S överensstämmer med valören på det översta kortet i hög 3! Hur ska man förklara att det här tricket är möjligt? |
|
Avståndsbedömning
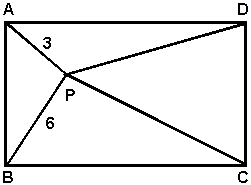
| Sträckorna PA
och PB är 3 resp. 6 cm. Avstånden (i cm) från punkten P till de övriga hörnen i rektangeln ABCD är också naturliga tal. Beräkna längden av sträckorna PC och PD! |
|
Biljardbollarna II
| I en låda ligger 12 biljardbollar. Alla ser likadana ut, och alla utom en av bollarna väger lika mycket. Går det att med hjälp av enbart en balansvåg (utan några vikter) hitta den felaktiga bollen på bara tre vägningar? |  |
|
|