Uppg. 1:
Adam ritar kvadrater, vilkas sidlängder är udda heltal.
Ett exempel finns i figuren till höger.
Kvadraten delas sedan in i små kvadrater så som bilden visar.
Därefter skuggas de diagonala små kvadraterna.
I en av Adams kvadrater är 196 små kvadrater vita.
Hur många små kvadrater finns det sammanlagt i den stora
kvadraten?
|
 |
Uppg. 2:
A, B och C kan var och
en gå med hastigheten
6 km/h.
De har också en motorcykel, som de kör med
hastigheten 90 km/h. Ingen hänsyn tas till extra
tid
vid start och stopp. Högst två av dem kan åka på
motorcykeln samtidigt. Alla tre ska ta sig till en
ort (X) 135 km bort.
a) Antag att A kör motorcykeln hela tiden. Han kör B
till orten X, vänder och hämtar upp C och kör sedan
till orten X. Hur lång tid tar det innan alla tre är
i orten X?
b) Vilken är den kortaste tiden för alla tre att ta
sig till orten X? |
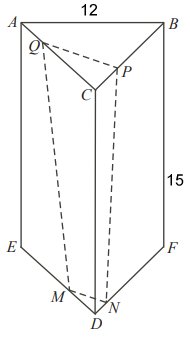 |
Uppg. 3:
Ett kompakt rakt prisma ABCDEF har höjden 15 cm
och basytor i form av liksidiga trianglar med sidan
12 cm.
Ett rakt snitt genom punkterna M, N, P och Q skär
bort kroppen QPCDMN. Beräkna volymen av denna kropp,
då DM är 4 cm, DN 2 cm och CQ 8 cm.
|
Uppg. 4:
Om talet 2k . 5300 skrivs ut som
ett vanligt tal utan potenser, innehåller det
303
siffror.
Vilken siffersumma har detta tal med 303 siffror, när k har
det minsta tänkbara heltalsvärdet?
|
Uppg. 5:
Emma ritar grafen till en andragradsfunktion, som saknar
konstant term.
Sedan ritar hon en likadan graf, som är parallellförflyttad
4 steg åt höger.
De båda graferna skär varandra i punkten (1,6).
a)
Vilken andragradsfunktion ritade Emma upp först?
b) Hur stor är arean som begränsas av x-axeln och de båda
graferna? |
|
|
|
|
|