|
Problem för hängmattan och badstranden del
I del
I
|
|
 |
|
serietabellen |
Några grabbar anordnar en fotbollsturnering under
sommarlovet.
Varje lag möter vart och ett av de andra
lagen fyra gånger.
De kallar lagen för IFE (IF
Elfsborg), MFF (Malmö FF), DIF (Djurgårdens IF) och BP
(Brommapojkarna).
När serien är färdigspelad har IFE
22 poäng, MFF 19 poäng, DIF 14 poäng och BP 12 poäng.
Hur många matcher slutade oavgjort?
Samma
poängfördelning för vunna, oavgjorda och förlorade
matcher som i det svenska seriesystemet. |
|
|
|
|
beviset |
Diagonalerna i en romb är d1
och d2.
Den i
romben inskrivna kvadratens sida är a.
Bevisa att
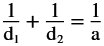
|
|
|
rutorna |

I alla rutor ska det stå ett heltal.
Efter den
tredje rutan, som innehåller siffran 6, gäller följande
regel:
Siffran i en ruta ska vara lika med summan av
de tre föregående rutornas heltal.
Bestäm vilka
heltal som finns i rutorna.
|
|
|
|
|
de tre sista
siffrorna |
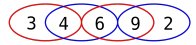
Talet ovan innehåller 5 siffror. Om vi väljer ut två på
varandra följande siffror får vi talen 34, 46, 69 och
92. De är alla delbara med 17 eller 23.
Antag
att ett heltal bestående av 2022 siffor börjar med
siffran 3 samt att två på varandra följande siffror
bildar ett tal som är delbart med 17 eller 23.
Vilka
är de tre sista siffrorna i detta tal med 2022 siffror? |
|
|
|
rektangeln |
I rektangeln ABCD är AB
= 5
dm och BC = 2 dm. På sidan AB ligger punkten
E. När man sammanbinder E med C och D, blir produkten av sammanbindningslinjernas
mätetal 10.
Bestäm punkten E:s läge.
Extrauppgift:
Ge exempel på en
rektangel, där såväl rektangelns sidor som
sammanbindningslinjerna är naturliga tal. |
|