Problem för hängmattan och badstranden del
I del
I  |
|
omkretsarna |
I
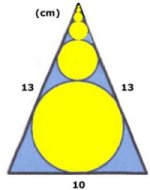
triangeln finns ett oändligt antal cirklar, som tangerar
de båda lika sidorna samt de närliggande cirklarna.
Hur stor är summan av omkretsarna
för alla cirklarnas ?
|
 |
|
|
Primtalen |
|
Antag att
man slumpmässigt väljer två primtal
bland de första tio primtalen.
Hur stor är sannolikheten att
a) summan av de båda primtalen är 24?
b) produkten av de båda primtalen är
jämnt delbar med 3? |
|
hundrametersloppet |
|
När Amanda
går i mål i ett hundrameterslopp, har
Sara sprungit 95 m.
Nästa gång startar de också samtidigt
men med Amanda 5 m bakom ordinarie
startlinje för att det ska bli ett
jämnare lopp.
a) Vem kommer först i mål?
Kan man avgöra det utan att göra några
detaljerade uträkningar?
b) Hur stort är avståndet mellan dem när
den första går i mål?
Vi förutsätter att de springer med
konstant fart (vilket egentligen är helt
orealistiskt) och att de håller samma
fart i första och andra loppet. |
|
cylindern |
|
En
cylinder med maximal volym är inskriven
i ett klot med radien R.
Beräkna förhållandet mellan klotets
volym och cylinderns volym. |
|
|
|
summan |
Talen a, b, c, d är
positiva heltal.
Följande samband gäller:
ab + cd = 38
ac + bd = 34
ad + bc = 43
Vad är värdet av a + b + c + d? |
|