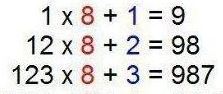Månadens problem juli 2017

Månadens problem
juli 2017

Problem för hängmattan och badstranden del 1

Uppg. 1

Mamma och pappa Sjöström har tre söner. Varje son har två systrar.
Hur många medlemmar består familjen Sjöström av?

Uppg. 2

I en karamellskål finns det 10 röda, 15 gula och 12 gröna påskägg.
Du plockar upp ägg utan att titta på färgen.
Hur många ägg måste du ta för att vara säker på att få alla tre sorterna?

Uppg. 3

Vid en etapp av Tour de France kom tre svenska åkare i mål. En av dem kom exakt på den mellersta platsen. De andra två svenska åkarna hamnade längre bak i prislistan, 42:a resp. 80:e plats. Hur många cyklister kom i mål på den här etappen?

Uppg. 4

Hur stor är vinkeln ABC i kuben till höger?

Uppg. 5

En vattenmelon, som väger 400 g, innehåller 95 % vatten. Tjugo dagar senare har andelen vatten sjunkit till 90 %. Hur mycket väger vattenmelonen då?

Uppg. 6

Kubens kanter är 4 cm. Man skär av alla hörn på kuben,
2 cm från resp. hörn (se figur)
Hur många hörn kommer den nya rymdfiguren att ha?

Uppg. 7

Den blå kvadraten har arean 81 cm²
Den stora kvadratens sida är x cm.
Hur lång är sträckan x?

Uppg. 8

Hur många vertikala snitt måste du minst göra för att dela kakan i åtta stycken lika delar?

Uppg. 9

Studera mönstret till höger.
Ange den räkneoperation som följer samma mönster och som ger ett svar med siffrorna 1-9 i fallande ordning.

Uppg. 10

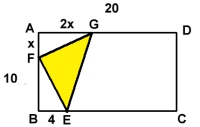
I rektangeln ABCD är AB=10 cm och AD= 20 cm.
E är en punkt på BC. Sträckan BE=4 cm.
Punkterna F och G ligger på AB resp. AD.
Sträckan AF=x cm och sträckan AG=2x cm.
Hur stor är den största möjliga arean av triangeln EFG?

Uppg. 11

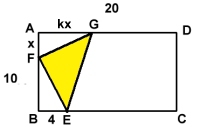
Generalisering av uppg. 10:
Sträckan AG = 2x ersätts av AG = kx
Undersök största möjliga area för triangeln EFG vid olika k-värden.
Vilket k-värde ger minsta värdet, när man beräknar största möjliga area för triangeln EFG? k > 0