|
Uppg. 1 |
|
Mamma och pappa Sjöström har tre söner.
Varje son har två systrar.
Hur många medlemmar består
familjen Sjöström av? |
Svar: 7 familjemedlemmar
De tre pojkarna har naturligtvis samma systrar.
Pappa, mamma, tre pojkar och två flickor =
sju familjemedlemmar.
|
|
|
Uppg. 2 |
|
I en karamellskål finns det 10 röda,
15 gula och 12 gröna påskägg.
Du plockar upp ägg utan att titta på färgen.
Hur många ägg måste du ta för att vara
säker på att få alla tre sorterna?
|
Svar: 28 ägg
Man skulle kunna ta 27 ägg och enbart
få gula och gröna ägg, men i så fall måste nästa ägg
vara rött! |
|
|
Uppg. 3 |
Vid en
etapp av Tour de France kom
tre svenska åkare i mål.
En av dem kom
exakt på den mellersta platsen.
De
andra två svenska åkarna hamnade
längre bak i
prislistan, 42:a resp. 80:e plats.
Hur många
cyklister kom i mål på den här etappen? |
Svar: 81 åkare
Den åkare som kom på den mellersta
platsen, har lika många åkare före som efter sig.
Eftersom han kom före svensken på 42:a plats kan han
sämst vara 41:a. Om han kom på 40:e plats skulle
antal åkare i mål vara 79 st., vilket är orimligt,
eftersom en av svenskarna kom på 80:e plats.
Nr 41 är alltså den mellersta platsen och antalet
cyklister i mål blir 40 + 1 + 40 = 81.
|
|
|
Uppg. 4 |
|
Hur
stor är vinkeln ABC?
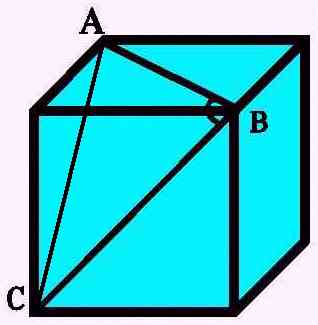 |
Svar: 60 grader
Triangeln ABC är liksidig.
Vinkeln ABC är därför 60 grader. |
|
|
Uppg. 5 |
|
En vattenmelon, som väger 400 g,
innehåller 95 % vatten.
Tjugo dagar senare
har andelen vatten sjunkit till 90 %.
Hur
mycket väger vattenmelonen då? |
Svar: 200 g
Eftersom vattenmelonen innehåller 95 %
vatten, väger melonens övriga beståndsdelar
5% av
400 g = 20 g. Tjugo dagar senare utgör
övriga beståndsdelar (100 - 90) % = 10 %.
Hela melonen väger alltså 10 * 20 g = 200 g. |
|
|
|
Uppg. 6 |
|
Kubens
kanter är 4 cm.
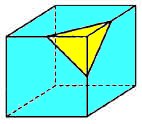
Man skär av alla hörn på kuben,
2 cm från resp. hörn
(se figur)
Hur många hörn kommer den
nya rymdfiguren att ha?
|
 |
Svar: 12 hörn
När man skär av ett hörn, bildas tre
nya hörn.
Av figuren framgår dock att man bara
får
ett
hörn på var och en av den gamla kubens kanter. |
|
|
Uppg. 7 |
|
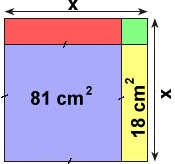
Den
blå kvadraten har arean
81 cm2
Den
stora kvadratens sida är
x cm.
Hur lång är sträckan x? |
 |
Svar: 11 cm
Den blå kvadratens area är 81
cm2.
Därför är sidan 9 cm.
Den långa sidan i den gula
rektangeln är då också
9 cm. Eftersom arean är 18cm2,
måste
den korta sidan vara 2 cm.
Den stora kvadratens sida blir därför (9 +
2) cm = 11 cm.
|
|
|
Uppg. 8 |
|
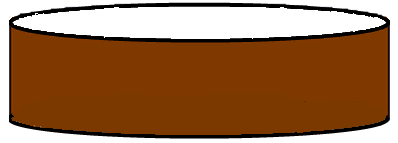
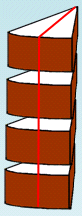
Hur
många vertikala snitt måste du minst göra för att
dela kakan i åtta stycken
lika
delar? |
 |
Svar: 3 snitt
1) Lägg två vinkelräta,
vertikala snitt.
2) Stapla de fyra bitarna ovanpå varandra
och
gör det tredje vertikala snittet!
OBS!
Lika delar.
Lägger
man ett horisontellt snitt, får man inte
åtta
lika
delar. |
|
|
Uppg. 9 |
|
Studera mönstret till nedan
Ange den räkneoperation som följer samma
mönster och
som ger ett svar med siffrorna
1-9 i fallande ordning
. |
Svar: 123456789 x 8 + 9 = 987654321
 |
|
|
Uppg. 10 |
|
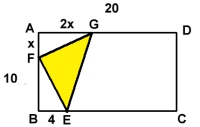
I rektangeln ABCD är
AB = 10 och AD = 20cm.
E är en punkt på BC. Sträckan BE=4 cm.
Punkterna F och G ligger på AB resp. AD.
Sträckan AF=x cm och sträckan AG=2x cm.
Hur stor är den största möjliga arean av triangeln
EFG?
 |
Svar: 36 cm2
Lösning:
Triangeln EFG:s area = arean av parallelltrapetset
ABEG:s area - arean av de två trianglarna AFG och
BEF.
f(x) = 10(2x + 4)/2 - 2x2/2 - 4 . (10 - x)/2
f(x) = 12x - x2
Vi deriverar med avseende på x och sätter derivatan
lika med noll.
f '(x) = 12 - 2x
f '(x) = 0
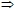 12 - 2x = 0
12 - 2x = 0
x = 6
Triangeln EFG:s area 12x - x2 = 12
. 6 - 62 = 36
|
|
|
Uppg. 11 |
|
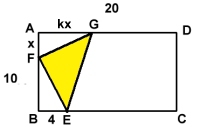
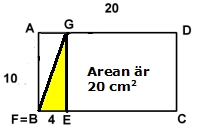
a)
Vilket förhållande mellan sträckorna AG och AF ger
den minsta arean för triangeln EFG?
Använd beteckningarna AF = x och AG = kx (se figur)
b) Hur stor är den arean?
 |
Svar: k,
dvs. förhållandet mellan AG och AF är 2/5.
Arean av triangeln EFG är då 20 cm2
Lösning:
Två villkor gäller
0< k ≤ 20/x (sidan AD)
0< x ≤ 10
(sidan AB)
Triangeln EFG:s area = arean av
parallelltrapetset ABEG:s area - arean av de
två trianglarna AFG och BEF. Sätt A =
arean av triangeln EFG
A = 10(kx + 4)/2 - kx2/2 - 4
.
(10 - x)/2
A = 5kx - kx2/2 + 2x
Vi deriverar med avseende på x och sätter
derivatan lika med noll.
dA/dx = 5k - kx + 2
dA/dx = 0
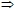 5k -kx + 2 = 0 5k -kx + 2 = 0
x = 5 + 2/k
x = 5 + 2/k insatt i villkoret 0< x ≤
10
ger 2/5 ≤ k
Sätt in x = 5 + 2/k (från ekv. (4)) i ekv.
(3)
Vi får då A = 25k/2 + 10 + 2/k
Derivering med avseende på k ger
dA/dk = 25/2 - 2/k2
När vi sätter derivatan lika med 0 får vi
k = 2/5
Eftersom andraderivatan är positiv, är det
ett minimum.
Detta minimum faller precis på gränsen för
de tillåtna värdena enligt enligt ekv. (2)
medan villkoret i ekv. (1) är väl uppfyllt.
Sätt in värdena för k och x i ekv. (3)
Arean av triangeln EFG blir då 20 cm2 |
(1)
(2)
(3)
(4)
(5)
(6)
(7) |
|