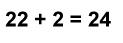Problem för hängmattan
och badstranden
 |
|
Den första
upplagan av Matematikboken (Författare: Undvall m. fl.) kom
redan på 70-talet. Nedanstående uppgifter är varianter på
uppgifter i Matematikboken åk 9. |
|
Uppg. 1 |
Fåraktigt
Bonden Per har satsat på fårskötsel.
Om han delar upp sina får i grupper med 2,
3, 4, 5 eller 6 får i varje grupp, blir det
alltid ett får över.
Om han däremot delar upp fåren i grupper med
7 i varje, blir det inget får över. Hur
många får har Per?
|
 |
|
|
Uppg. 2 |
Tre
likadana siffror
Talet 24 kan skrivas med tre likadana siffror på det
här sättet: 22 + 2 = 24.
Kan du hitta två andra möjligheter? |
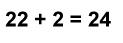 |
|
|
Uppg. 3 |
Äpplena
När Lars, Erik och Sven träffades, hade Lars
3 äpplen och Erik 5 äpplen.
Äpplena delades lika mellan alla tre.
Eftersom Sven inte hade några äpplen med
sig, betalade han 8 kr.
Hur ska denna summa fördelas mellan Lars och
Erik? |
 |
|
|
Uppg. 4 |
Punkteringen
Uno låg vid vägkanten och latade sig, när
tävlingscyklisten Kajsa susade förbi på sin
träningsrunda med hastigheten 10 m/s. Efter 14 s
hörde han en dov smäll och förstod att Kajsa hade
fått punktering.
Hur stort var avståndet då mellan Uno och Kajsa, om
Kajsa stannar direkt efter punkteringen?
Ljudets hastighet är 340 m/s.
|
 |
|
|
Uppg. 5 |
Den
sista siffran
Med vilken siffra slutar talet 2100 om man
skriver ut hela talet utan potenser?
|
 |
|
|
Uppg. 6 |
De
falska mynten
Sultanen har dömt en av sina underlydande till
döden.
Den dödsdömde har dock en chans att bli
benådad:
Han ska lösa följande problem med en enda vägning
med en noggrann digital våg:
På bordet ligger tio travar med 10 mynt i varje
trave. En av travarna innehåller bara falska mynt.
Ett äkta mynt väger 10 gram och ett falskt mynt 9
gram.
Hur ska den dödsdömde gå tillväga? |
 |
|