|
TOMTENS JULKLAPPSSÄCK |
Tomtefar: I min julklappssäck finns mellan
20 och
100 julklappar.
Om man kastar om siffrorna i antalet julklappar får man ett primtal.
Tomtemor: Jag behöver fler ledtrådar.
Tomtefar: Om jag hade haft ytterligare en julklapp, hade antalet varit
delbart med 5.
Tomtemor: Jag behöver en ledtråd till!
Tomtefar: Om jag hade haft en julklapp mindre, hade antalet julklappar
varit ett primtal.
Tomtemor: Nu vet jag svaret!
Hur många julklappar fanns det i tomtens säck? |
 |
|
|
silversmycket |
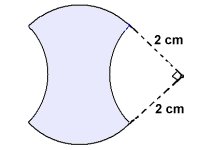
I tomteverkstaden satt en tomtenisse och tillverkade
silversmycken (Se figur). Smyckets omkrets består av cirkelbågar.
a) Vilket villkor måste figuren uppfylla för att nedanstående uppgifter ska gå att
lösa?
b) Hur stor är arean av smyckets framsida?
c) Hur stor är omkretsen av smycket?
|
 |
|
|
Under en lektion fick tomtenissarna lösa kryptogram. Här kommer ett exempel:
7(JULMYS) = 6(MYSJUL)
Varje bokstav ska ersättas med en viss
siffra.
Lös kryptogrammet. |
|
multiplikationen |
|
a)
|
Tomtefar har numera kvinnliga
tomtenissar.
Alma är en av dem. När
hon snabbt hade klarat av grundkursen i matematik, fick hon lära
sig att använda andra talsystem.
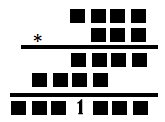
I uppgiften till höger är multiplikationen skriven i det binära
talsystemet.
Alma klarade snabbt av att ersätta de svarta kvadraterna med
ettor och nollor och det klarar du väl också? |
 |
|
b) |
När Alma var klar med a-uppgiften, sa läraren:
- Om man skriver ditt svar i ett annat talsystem, blir svaret
113. Vilket är talsystemet? |
|
c) |
Har talsystemet i b-uppgiften använts i något praktiskt
sammanhang? |
|
mattelektionen |
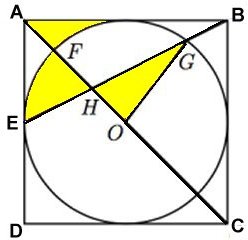
En cirkel med medelpunkten O är inskriven i en kvadrat med sidan 6 cm.
E är mittpunkt på sidan AD.
Tomtenissarna hade i uppgift att beräkna differensen mellan kvadratens
och cirkelns area, men tomtenissen Albin, som bara satt och tänkte på
julafton, började färglägga delar av figuren.
Ange det exakta värdet för den area, som han hade färglagt (se fig.), när läraren upptäckte honom. |
 |
|
|
|