|
Månadens
problem |
Problem för hängmattan
och badstranden |
|
|
geometrisk formel |
|
|
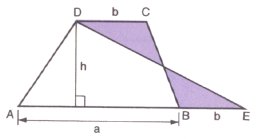
Vilken geometrisk formel
skulle vi kunna få fram med hjälp av den här figuren? |
 |
|
KUl matematik |
|
|
Vilka
tresifffriga tal KUL uppfyller
ekvationen |
|
|
Parallelltrapetset |
|
|
I ett likbent parallelltrapets är en
av de parallella sidorna 12 cm och summan av de övriga
sidorna 24 cm. Hur långa är de okända sidorna, när trapetsets area är så stor som möjligt? |
|
|
lackeringen |
|
|
Isabelle började lackera sin
leksakshelikopter mellan kl. 9.00 och 10.00. När hon var klar mellan kl. 10.00 och 11.00, hade minutvisaren och timvisaren bytt plats jämfört med när hon började lackera. Hur lång tid tog lackeringen? Avrunda svaret till hela minuter. |
|
|
Kortspelet |
|
 |
|
|
Adam och Bianca spelar ett kortspel.
Adam har sex kort, 2 från Röda familjen, 2 från
Brillfamiljen och 2 från Kungafamiljen. Bianca har fyra kort, 2 från Rosa familjen och 2 från Muntra familjen. Adam och Bianca turas om att slumpmässigt lägga ut ett kort. Kortet ligger sedan kvar på bordet under återstoden av spelet. Adam börjar. Den spelare, som först har lagt ut 2 kort från samma familj, vinner. Beräkna sannolikheten att Adam vinner. |
|