|
Månadens
problem |
Problem för hängmattan
och badstranden |
|
|
Uppg. 1: Ett tåg bestod av fem vagnar. I varje vagn fanns det minst en passagerare. Två passagerare kallas "grannar", om de sitter i samma vagn eller i vagnarna närmast intill varandra. Varje passagerare hade fem alternativt tio grannar. a) Hur många passagerare fanns det på tåget? b) Hur många passagerare satt i den mellersta vagnen? |
|
|
Uppg. 2: Talet x = 999...999 består av 999 st nior. Hur stor är siffersumman i talet x2 |
|
|
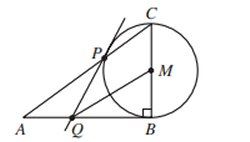
Uppg. 3: Triangeln ABC är rätvinklig. Punkten M på sidan BC är medelpunkt för en cirkel med BC som diameter. Cirkeln skär sidan AC i punkten P. Tangenten till cirkeln i punkten P skär sidan AB i punkten Q. Bevisa att QM är parallell med AC. |
 |
|
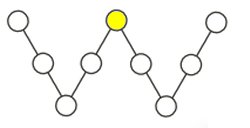
Uppg. 4: Det största av nio på varandra följande heltal är 2020. Dessa nio heltal är placerade i cirklarna till höger. Summan av de tre heltalen längs var och en av de fyra linjerna är densamma. Vilket tal ska stå i den gula cirkeln, om summan ska vara så liten som möjligt? |
 |
|
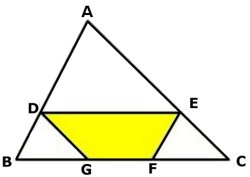
Uppg. 5: I figuren till höger är arean av triangeln ABC 1 a.e. I parallelltrapetset DEFG är DE parallell med BC, EF parallell med AB och DG parallell med AC. Bestäm den maximala arean av parallelltrapetset DEFG!
|
 |