|
Månadens
problem |
Problem för hängmattan
och badstranden |
|
|
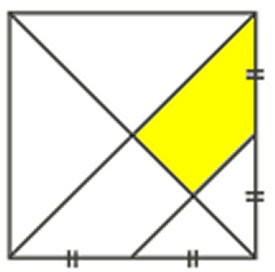
Uppg. 1: Hur stor del av hela kvadraten är färgad gul? |
 |
|
Uppg. 2: Professor Kalkyl gav sina elever i uppgift att skriva upp alla tal med följande egenskaper: ● talet är femsiffrigt ● alla siffrorna är olika ● den första siffran är lika med summan av de övriga siffrorna Hur många tal med dessa egenskaper finns det? |
|
|
Uppg. 3: Sannolikheten för tre studenter, Bertil, Alice och Christer, att klara sin examen bedöms vara respektive 0,4 0,5 och 0,7. Hur stor är sannolikheten för att åtminstone en av dem ska klara examen?
|
 |
|
Uppg. 4: När professor Kalkyl gick i skolan skrev han vid ett tillfälle ett tvåsiffrigt tal. Sedan bildade han ett nytt tvåsiffrigt tal genom att kasta om siffrorna i det första talet. Till sin förvåning fann han att summan av de båda talen var en jämn kvadrat. Finn alla tvåsiffriga tal som man kan börja på, för att summan i den ovan beskrivna beräkningen ska bli en jämn kvadrat. Genomför också ett bevis. |
|
|
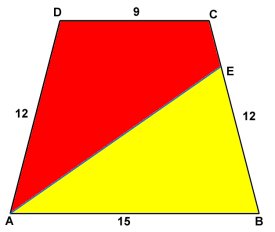
Uppg. 5: I ett likbent parallelltrapets ABCD är AB och CD 15 resp. 9 cm. De icke parallella sidorna är vardera 12 cm. Bisektrisen till vinkeln A skär sidan BC i punkten E. Beräkna förhållandet mellan den röda och den gula arean utan att använda trigonometri. |
 |
Extrauppgift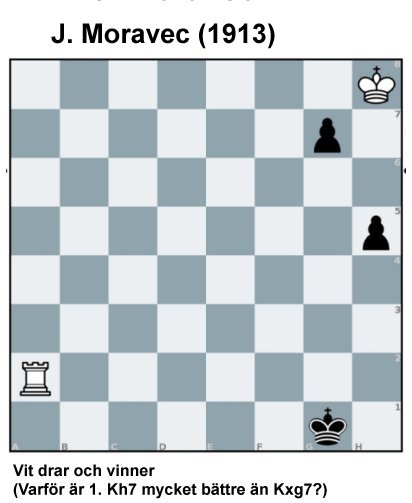 |
|