Ex.
1:
Svar:
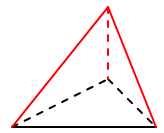
Låt de sex
tändstickorna bilda en tetraeder. |
 |
Ex.
2:
Svar:
16 cm2
Lösning:
De blå delarna som ligger utanför den gula
kvadraten motsvaras av de blå figurerna innanför kvadraten.
Utanför kvadraten finns dessutom två röda halvcirklar. Den
ursprungliga rödfärgade figurens area
är därför lika stor som den gula kvadratens area + arean av en
cirkel.
Cirklarnas radie är 1 cm. Därför är kvadratens sida 4 cm
A = (4 . 4 +
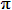 )cm2 = 16
+ )cm2 = 16
+ 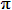 cm2 cm2 |
 |
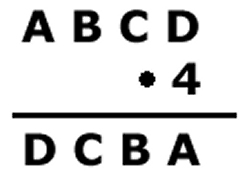
Ex. 3:
Svar:
A = 2, B = 1 C = 7 och D = 8
|
 |
Lösning:
Eftersom det inte blir någon minnessiffra när man multiplicerar
4 . A i tusentalskolumnen, måste A motsvara 1
eller 2.
Av entalskolumnen framgår att A är ett jämnt tal. Då är A = 2
Då måste D vara lika med 3 eller 8.
4 . A = D i tusentalskolumnen innebär att D =
8 (D kan inte vara 3).
4 . B i hundratalskolumnen ger ingen
minnessiffra. Då måste B = 1
4 . C i tiotalskolumnen ger då en produkt med
entalssiffran 1, sedan man lagt till minnessiffran 3 från
entalskolumnen. Det värde som då passar in på C är 7. |
Ex. 4:
Svar: 25
Givet:
x - y = 3 och xy = 8
Lösning:
x - y = 3
Kvadrera båda leden!
x2 - 2xy + y2 = 9
x2 + y2 = 9 +
2xy
men xy = 8
x2 + y2 = 9 +
2
. 8 = 25
|