Geometri: Ett överraskande resultat!?

Material: Ett stort papper, t.ex. en tidningssida, linjal och penna.

1.	Tag ett stort papper och vik det, så att en oregelbunden fyrhörning bildas.
2.	Märk ut mittpunkten på  varje sida. Du kan göra det genom att mäta med en linjal eller genom att vika fyrhörningen så att två närliggande hörn kommer över varandra.
3.	Varje mittpunkt ska nu sammanbindas med närliggande mittpunkter, så att en ny fyrhörning bildas.
4.	Vilka egenskaper har den nya fyrhörningen?
	Svar

Några andra matematiklaborationer:

Kors i kvadrat.htm

a4.htm

Svar: Den nya fyrhörningen är en parallellogram.
Bevis:
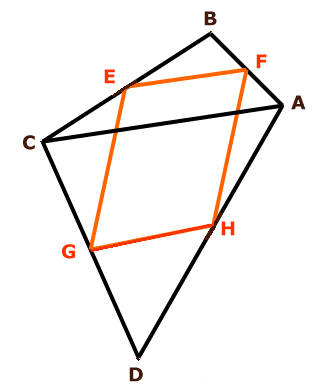
Figuren EFGH förefaller att vara en parallellogram. Kan vi bevisa det?
1.	E, F, G och H är mittpunkter på resp. sida.
2.	Triangeln BEF är likformig med triangeln ABC, eftersom vinkeln B är gemensam och BE hälften så lång som BC och BF hälften så lång som BA.
3.	Då är EF parallell med CA.
4.	Med samma resonemang kan man visa att triangeln DGH är likformig med triangeln ACD.
5.	Därför är GH parallell med CA.
6.	Då måste också sidorna EF och GH vara parallella!
7.	Nu återstår att visa att EG och FH är parallella, men eftersom man då tillämpar samma metod som i punkterna 1-6 är det en enkel match.
8.	Slutsats: Motstående sidor är alltså parallella. Det är ju just det som är definitionen på en parallellogram!

Tillbaka