Temat "A4-papperet"

Material: Ett A4-papper, linjal och gradskiva.

Ett A4-papper har måtten 210 x 297 mm

Uppg. 1: Dividera långsidans mått med kortsidans, dvs. 297/210

Svaret blir 1,414...

Det är svaret verkar bekant eller hur?	()
Det innebär att förhållandet mellan kortsida och långsida är

Uppg. 2: Vik A4-papperet på mitten längs den röda linjen.

Du får då ett papper i A5-format.
Är förhållandet mellan kortsida och långsida fortfarande		?

Svar: Ja, så är det för alla format av den här typen (A1, A2, A3, A4 osv.)

Slutsats: Arean av A5 är hälften av arean av A4.
             Arean av A4 är hälften av arean av A3 osv.

Uppg. 3: Arean av A0 är 1 m².
             Hur stor är arean av ett A4-papper? Ange svaret i bråkform.
             Svar: Om man viker ett A0-papper till ett A4-papper halverar man arean 4 gånger.
             1/2⁴m²= 1/16 m²

Uppg. 4: Att vika ett A4-papper så att man får en liksidig triangel.
1) Rita en hjälplinje på A4-papperet. Se fig.

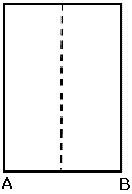
2) Vik papperet längs en linje AD, så att hörnet B hamnar på den streckade hjälplinjen i punkten C. (se fig.)

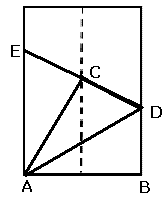
3) Vik nu papperet längs linjen DE (se fig. ovan)
    Då kommer det att se ut så här:

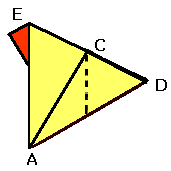
4) Nu återstår bara att vika in den röda triangeln.

5) Undersök om den gula triangeln verkar vara en liksidig triangel genom att mäta sidorna eller vinklarna.

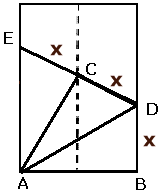
6)	Bevis för att triangeln ADE verkligen är en liksidig triangel:
	Eftersom hörnet B vid den första vikningen hamnar i punkten C, är BD = CD och AC = AB. Med likformighet kan man visa att CE = CD. Eftersom vinkeln B är 90^o, är också vinklarna ACD och ACE 90^o. Trianglarna ABD, ACD och ACE är kongruenta (Första kongruensfallet: två sidor och mellanliggande vinkel) Det innebär att vinkeln A är är delad i tre lika stora delar, dvs. varje del är 90^o/3 = 30^o. Nu är det lätt att visa att alla tre vinklarna i triangeln ADE är 60^o, dvs. triangeln ADE är liksidig.

Några andra matematiklaborationer:

Kors i kvadrat.htm

fyrhorning.htm