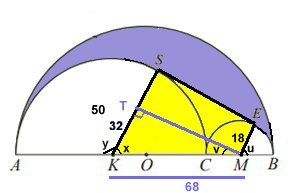
Fältarbete (lösning)
Svar: 2040 cm2
Lösning:
OC = 32 cm
CB = 36 cm.
OC = radien i den största halvcirkeln =
36 cm + 32 cm = 68 cm
CM = radien i den minsta halvcirkeln =
36/2 cm = 18 cm
KC = radien i den tredje halvcirkeln =
(2 . 68 - 2 . 18)/2 cm =50 cm
KMES är ett parallelltrapets. Eftersom SE är en tangent är vinklarna vid S och E räta.
För att beräkna parallelltrapetsets yta behöver vi veta längderna av KS, ME och SE.
KS = KC = 50 cm och ME = CM = 18 cm.
Pytagoras sats på triangeln KMT ger
MT = 60 cm SE = MT = 60
Parallelltrapetsets area är
60(50 + 18)/2 cm2 = 2040 cm2
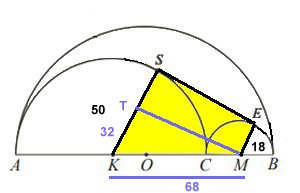
Svar: Arean av det blå området är
2470 cm2
Lösning:
Vi böjar med att beräkna vinklarna v, u, x och y.
arcsin v = 32/68 v ≈ 28,1o
Då är
u = 180o - 90o - 28,1o = 61,9o
x = 90o - 28,1o = 61,9o
y = 180o - 61,9o = 118,1o
Det blå området=
arean av den största halvcirkeln - det gula området - cirkelsektorn med medelpunktsvinkeln y -cirkelsektorn med medelpunktsvinkeln u
Arean av den största halvcirkeln
Arean av cirkelsektorn med medelpunktvinkeln y
Arean av cirkelsektorn med medelpunktvinkeln u
Det blå området =
(2312
(1436