|
Månadens
problem |
|
kycklingarna |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Svar: Bonden
Josef har 300 kycklingar. Lösning: Antag att fodret f.n. räcker till x kycklingar under y dagar, dvs. antalet dagsportioner är xy (1) Alternativ 1: 75 kycklingar säljs Antal dagsportioner: xy = (x - 75)(y + 20) (2) Alternativ 2: 100 kycklingar köps in. Antal dagsportioner: xy = (x + 100)(y - 15) (3) Ekv.: |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
palindromtal |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Svar: 45
femsiffriga
palindromtal är delbara med 37 Lösning: En enkel programmering kan se ut så här: 10 S = 0 20 FOR A = 1 TO 9 30 FOR B = 0 TO 9 40 FOR C = 0 TO 9 50 T = 10000*A + 1000*B + 100*C + 10*B + A 60 IF T/37 = INT(T/37) THEN PRINT T;: LET S = S + 1 70 NEXT C 80 NEXT B 90 NEXT A 100 PRINT 110 PRINT S;" Antalet femsiffriga palindromtal, som är delbara med 37." Några förklaringar: Det femsiffriga talet T skrivs 10000*A + 1000*B + 100C + 10*B + A S är antalet femsiffriga palindromtal, som är delbara med 37.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
schackbrädet |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Svar: Nej, det går
inte. Lösning: Två vita rutor togs bort. Då återstår 30 vita och 32 svarta rutor. Varje dominobricka täcker en vit och en svart ruta! Hur man än lägger de 30 första brickorna kommer de därför att täcka 30 vita och 30 svarta rutor. Då har man kvar en dominobricka och två svarta rutor. Eftersom två rutor intill varandra (vågrätt eller lodrätt) alltid har olika färg kan man inte täcka de två kvarvarande svarta rutorna med den återstående dominobrickan. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
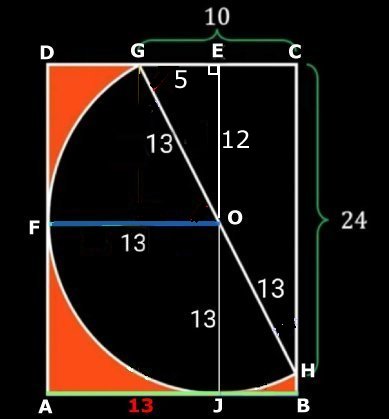
Rektangeln |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
den okända arean |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
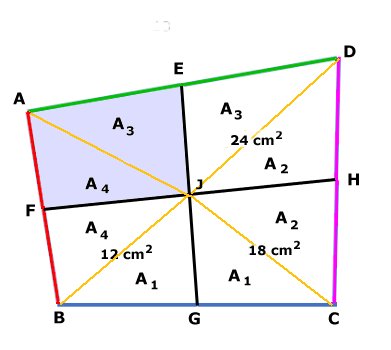
Svar: Arean av fyrhörningen AFJE är 18 cm2. Lösning: Fyrhörningen ABCD består av fyra mindre fyrhörningar. Rita in diagonalerna AJ, BJ, CJ och DJ i dessa fyrhörningar. Trianglarna med beteckningarna A1 har lika stora areor, eftersom de har lika stora baser och en gemensam höjd. Motsvarande resonemang gäller för areorna A2, A3 och A4. Det ger ekvationerna A1 + A2 = 18 (1) A2 + A3 = 24 (2) A1 + A4 = 12 (3) Ekv. (1) och (2) ger A1 = A3 - 6 Då kan ekv. (3) skrivas A3 - 6 + A4 = 12 A3 + A4 = 18 (= AFJE) |
 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Du kan mejla din
lösning till mig (alf@mathpuzzle.se) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||