Uppg. 1:
Svar:
1/4
Lösning:
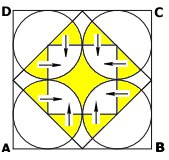
Flytta 8 av de gula områdena så att den minsta
kvadraten blir färgad gul.
Den minsta kvadratens area är 1/4 av kvadraten
ABCD:s area
|
 |
Uppg. 2:
Svar: 13 palindromer
Lösning:
Delbarhet med 6 innebär att palindromerna måste
vara jämna tal.
Då är tusentalssiffran (och entalssiffran) är jämna
tal.
I de här palindromerna är siffersumman delbar med 6.
2000 - 2999: 2112, 2442, 2772
4000 - 4999: 4224, 4554, 4884
6000 - 6999: 6006, 6336, 6666, 6996
8000 - 8999: 8118, 8448, 8778 |
Uppg. 3:
Svar:
Rektangelns sidor är 24 cm och 9 cm. |
Lösning:
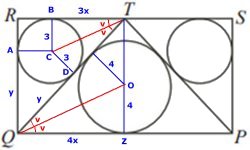
Vinklarna PQT och RTQ är lika stora (alternat-vinklar).
OQ och CT är bisektriser till dessa vinklar.
Därför är de fyra vinklarna v (se fig.) lika stora.
Då är trianglarna BCT och ZOQ likformiga.
Förhållandet mellan BT och QZ är 3:4 eftersom förhållandet
mellan radierna BC och OZ är 3:4.
Vi betecknar BT med 3x och QZ med 4x.
RT = QZ: RT är 3x + 3 och QZ = 4x.
Ekv.: 3x + 3 = 4x x = 3 |
 |
Sidan
RS = 3 + 3x + 3x + 3 = 3 + 3 .
3 + 3 . 3 + 3 =
24 (cm)
AQ = QD betecknas med y.
Pythagoras sats på triangeln QRT:
Kateten RT = 12 (hälften av sidan RS)
Kateten RQ är 3 + y
DT = BT = 3x
Då är hypotenusan QT = y + 3x = y + 3 . 3
= y + 9
122 + (3 + y)2 = (y + 9)2
144 + 9 + 6y + y2 = y2 + 18y +
81
72 = 12 y
y = 6
Sidan RQ är 3 + 6 =
9 (cm) |
|
|
Uppg. 4:
Svar: a = 4
Lösning: |
|
ab= ab
(1)
a/b= a3b (2)
Multiplicera de två ekvationerna ledvis
ab . a/b = ab .
a3b
a2 = a4b
Exponenterna ger likheten 2 = 4b b=
1/2
b = 1/2 insatt i ekv. (1) ger a/2 = a1/2
Kvadrera!
a2/4 = a
a = 4
|
|
Uppg. 5:
a)
Svar: Ja
Lösning:
Fall 1:Adam tar en kula.
Om Britta tar 2 kulor och Cissi 1 kula (eller
tvärtom), måste Adam ta den femte kulan.
Fall 2: Adam tar två kulor.
Om Britta och Cissi tar var sin kula, måste Adam ta
den femte kulan.
b)
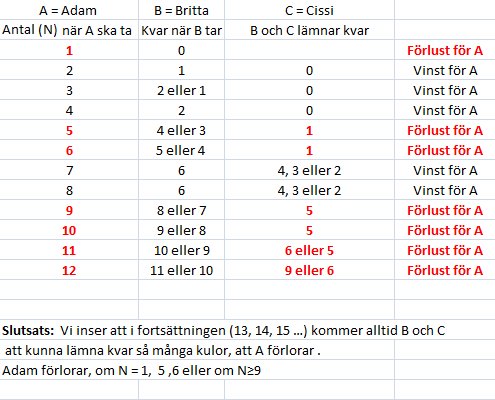
Svar: Adam förlorar när antalet kulor är 1, 5, 6
och N ≥
9
Lösning:
 |
|


