Uppg. 1:
Svar: 50 g
Lösning:
Antag att den tomma burken väger x gram och att ölet i en
full burk väger y gram.
Lös ekvationssystemet
x + y = 546 (1)
x + 0,5y = 298 (2)
Genom att subtrahera ledvis (1) - (2) får vi
0,5 y = 248
y = 496
x = 546 - 496
x = 50 |
Uppg. 2:
a)
Svar:
Vätskeytan ligger ≈
3,36 cm från botten.
Lösning:
Staffan R. har föreslagit följande lösning
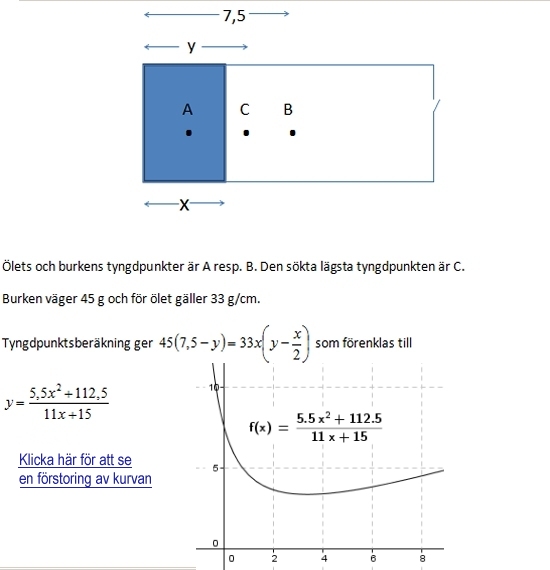
Ur diagrammet ser vi att tyngdpunkten ligger som lägst ca 3,36
cm över burkens botten och på samma nivå som ytan på ölet. Ölet
väger då ca 111g. |
|
Agne B. skriver:
Uppgift 2a är intressant.
Tomburken “väger” 3 g/cm och ölet 33 g/cm. Ölhöjd
x cm och tyngdpunktens höjd y cm. Vi låtsas att ölet är i fast
form och lägger ned burken. Tomburken och ölets vridmoment runt
tyngdpunkten lika stora och motriktade gav en
andragradsfunktion. Grafisk lösning på räknaren gav x=y ! Båda
ca 3,36 cm. Derivatan av en kvot och f´(x)=0 gav en
andragradsekvation och det exakta värdet. |
|
Gäller det alltid att den lägsta möjliga tyngdpunkten ligger i
vätskeytan?) |
|
Är lägsta
möjliga tyngdpunkt fördelaktigt för burkens stabilitet? |