Uppgift 1:
|
Svar: HE = 25 och SHE = 625 |
 |
Lösning:
Eftersom SHE är ett tresiffrigt tal, motsvarar HE ett
tal i intervallet 10-31. (102 = 100 och 312
= 961)
HE och SHE har samma sista siffra. SHE är dessutom en jämn
kvadrat. Sista siffran måste därför vara 0, 1, 5 eller 6.
1. HE = 10, 20 och 30 kan vi direkt utesluta, eftersom de
två sista siffrorna i SHE ska vara olika.
2. HE = 11, 21 och 31 fungerar inte heller.
3. HE = 15 är inte en lösning men däremot HE = 25 (252
= 625)
4. HE = 16 och 26 fungerar inte. |
|
Uppgift 2:
|
Svar:
ER = 19 och SIE = 361 |
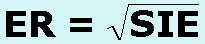 |
Lösning:
Även i det här fallet motsvarar ER ett tal i
intervallet 10-31.
E = 1, 2 eller 3 uppfyller det villkoret. Men eftersom SIE
är en jämn kvadrat, måste E vara en etta. (Ingen jämn
kvadrat har en tvåa eller en trea som sista siffra.)
Om en kvadraten på ett tal har en etta som sista siffra,
måste talet självt ha en etta eller en nia som sista siffra.
Ettan är redan upptagen (E = 1), dvs. R = 9
192 = 361 |
Uppgift 3:
Svar: Det finns två lösningar!
KAL = 164 och ADA = 656 eller
KAL = 169 och ADA = 676 |
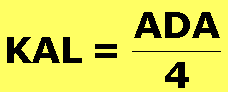 |
Lösning:
KAL motsvarar talet 100*K + 10*A + L och ADA talet 100*A
+ 10*D + A
Enl. uppg. är 4(100*K + 10*A + L) = 100*A + 10*D + A
Efter förenkling får man 61A = 400K + 4L - 10D
K = 1 eftersom K = 2 innebär att A>9
Om vi sätter in K = 1 får vi efter förenkling att A = (400 +
4L - 10 D)/61
Eftersom täljaren ska vara delbar med 61, undersöker vi den
kan vara 305, 366 eller 427. Vi inser direkt att värdet 305
är för litet och värdet 427 för stort.
Då återstår att undersöka värdet 366.
1) D =5 och L = 4 ger 400 + 4L - 10 D = 400
+4*4 - 10*5 = 366
2) D =7 och L = 9 ger 400 + 4L - 10 D = 400
+4*9 - 10*7 = 366
I båda fallen är A = 6 (366/61 = 6) |
|
|