a)
|
Svar: Om kvadraterna har sidorna 5
och 1 cm eller
4 och 2 cm är den sammanlagda omkretsen 24 cm.
Lösning: Summan av en sida i den röda kvadraten och en sida i den
blå kvadraten är 24/4 cm = 6 cm.
Eftersom kvadraterna är olika stora återstår bara två
alternativ: 5 cm och 1 cm eller 4 cm och 2 cm. |
 |
b)
|
Svar: Den sammanlagda arean kan
inte vara 17 cm2.
Lösning:
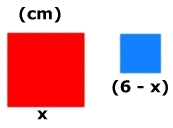
Antag att den röda kvadraten sida är x cm och den
blå kvadratens sida är
(6 - x) cm
Vi undersöker om den sammanlagda arean kan vara 17 cm2
genom att ställa upp ekvationen
x2 + (6 - x)2 = 17
Efter förenkling får vi
x2 - 6x + 9,5 = 0
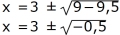
Eftersom talet under rotmärket är negativt, saknas reella lösningar |
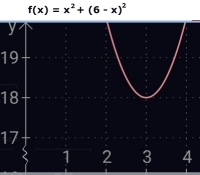
Anm. 1: Grafen till funktionen x2
+ (6 - x)2 visar
att minsta tänkbara sammanlagd area är 18 cm2
|
 |
|
Anm. 2: Med ett kalkylprogram kan man enkelt visa att
minsta tänkbara sammanlagd area är 18 cm2.
Arean 17 cm2 är därför inte tänkbar.
Anm. 3: En alternativ lösning är att bilda funktionen f(x) = x2 + (6 - x)2
Derivering ger att f'(x) = 2x + 2(-1)(6 - x)
f'(x) = 4x - 12
f'(x) = 0  4x - 12 = 0 x = 3
4x - 12 = 0 x = 3
Genom teckenstudier eller andra derivatan kan man visa att
x = 3
ger en minimipunkt.
x = 3  f(x) = x2 + (6 - x)2 = 9 + 9 =
18 f(x) = x2 + (6 - x)2 = 9 + 9 =
18
Den sammanlagda areans minimivärde är 18 cm2. Den
sammanlagda arean kan därför inte vara 17 cm2. |