Månadens problem juni 2017

Månadens problem
juni 2017 (lösning)

Grannarna

Svar:
Gatunummer
Adam: 2
Bertil: 3
Cissi: 5
Doris: 6
Erik: 12
Bertil och Cissi har angränsande tomter

Lösning:
Antag att Bertils gatunummer är b
              Cissis gatunummer är c
              Doris gatunummer är d
Ekv.:
2bc = 30      (1)
bcd = 90      (2)
12cd = 360   (3)

Om vi jämför ekv. (1) och (2) får vi d = 6
d = 6 insatt i ekv. (3) ger c = 5
c = 5 insatt i ekv. (1) ger b = 3

Rektangulärt papper

Svar: 32 cm²
Lösning: Rektangelns area är 64 cm².
Fyrhörningen CNMD har flyttats till ANMD’
Fyrhörningarna ANMD’ och AMNB är kongruenta.
Bevis: I båda fyrhörningarna finns triangeln AMN. Dessutom är trianglarna ABN och AD^´M kongruenta enligt tredje kongruensfallet:
En sida och två motsvarande vinklar ( B= D^' och BAN = D^'AM)
Arean av fyrhörningen ANMD’ är därför 64/2 cm² = 32 cm².

Staffan R. har hittat en elegant lösning:

Tärningarna

Svar:
a) Vid udda antal tärningar är summan de synliga prickarna delbar med sju.

b) Amanda klistrade ihop 19 tärningar.

Lösning:
a)
Det sammanlagda antalet prickar på en tärnings två motsatta sidor är alltid 7 och det totala antalet prickar på en tärning är 21.
Vi undersöker två, tre, fyra och fem ihopklistrade tärningar

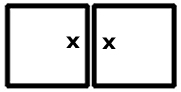Antal synliga prickar: 2 ^. 21 - 2x

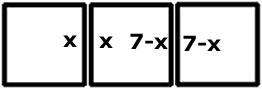Antal synliga prickar: 3 ^. 21 - 2 ^. 7

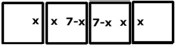Antal synliga prickar: 4 ^. 21 - 2 ^. 7 - 2x

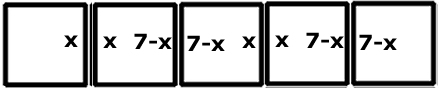Antal synliga prickar: 5 ^. 21 - 4 ^. 7

Slutsats: Vid udda antal tärningar är antalet synliga prickar delbart med 7.
Antalet synliga prickar när det är ett udda antal tärningar:
21n - 7(n -1) = 14n + 7 n = antalet tärningar
Antalet synliga prickar i Amandas stapel var 273.
273/7 = 39
Det är alltså ett udda antal tärningar.

b)
För antalet synliga prickar gäller då formeln 14n + 7
n = antalet tärningar
Ekv.: 14n + 7 = 273
n = 19