Månadens problem
juli 2018 (lösning)
Problem för hängmattan och badstranden   del 1     

Uppgift

Svar

Uppg. 1:
På en gata finns det tio lyktstolpar utplacerade med jämna mellanrum, varav en lyktstolpe finns i början av gatan och en finns i slutet.

På en annan gata finns det 100 lyktstolpar placerade på samma sätt som på den första gatan.
Hur många gånger så lång är den andra gatan jämfört med den första gatan?

 Svar: Den andra gatan är 11 gånger så lång.

På den första gatan finns det 10 lyktstolpar. Det betyder 9 mellanrum mellan lyktstolparna. På den andra gatan finns det med samma resonemang 99 mellanrum. Den andra gatan är alltså 11 gånger så lång som den första gatan.
 

Uppg. 2:
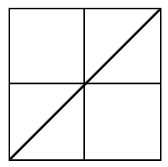
a) Hur många trianglar resp. kvadrater finns det i figuren till höger?

b) Vilket är förhållandet mellan trianglarnas och kvadraternas sammanlagda areor?
Svar: 3/4

 a)
Svar: Det finns sex trianglar och fem kvadrater.

b)
Svar:  Förhållandet är 3/4

Trianglarna: Fyra små trianglar är tillsammans häften av den stora kvadraten.
De två stora trianglarna täcker hela den stora kvadraten.
Sammanlagt: 1/2 + 1 = 3/2 (av den stora kvadraten)
Kvadraterna:
De fyra små kvadraterna täcker hela den stora kvadraten
Sammanlagt: 1 +1 = 2
Förhållande:

Uppg. 3:
Hur stor del av triangeln ABC är svart?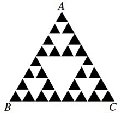

 Svar: 27/64

 

Uppg. 4:
Räkneoperationen definieras så här:
 


Vad är värdet av ?   		Svar: 79

= 2 (25 - 52) =
 2 7 = 27 - 72 = 128 -49 = 79

Uppg. 5:
 
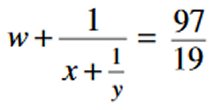x, y och w är positiva heltal.
Beräkna värdet av x, y och w med hjälp av ekvationen till höger.
 		 Svar: x = 9 y = 2  w =5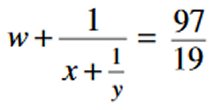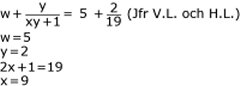
 

Uppg. 6:
En Mercedes Van med hastigheten 100 km/h och en Kia med hastigheten
80 km/h är på väg till Alphaville.
Mercedes Van kör om Kia:n 10 minuter innan  Kia:n är framme i Alphaville.
Hur mycket senare kommer Kia:n till Alphaville jämfört med Mercedesbilen?

 

 Svar: 2 minuter

Avstånd från omkörningspunkten till Alphaville:
Vi använder formeln s = v . t
Antag att sträckan tar x min för Mercedesbilen.
Ekv.: 100 . x/60 = 80 . 10/60
                   x = 8

Tidsskillnad: 10 min - 8 min = 2 min
 

Uppg. 7:
A och B är positiva heltal
Bestäm deras värde med hjälp av algoritmen till höger.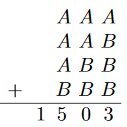

 		Svar: A = 2  B = 7 

A < 5 (hundratalskolumnen)

Studera entalskolumnen:
Fall 1:
A = 4 och B = 3
Kontroll:
444 + 443 + 433 + 333 = 1653
Duger inte!
Fall 2:
A = 3 ger inte ett heltalsvärde på B alt.
B = 0
Duger inte!
Fall 3:
A = 2 och B = 7
222 + 227 + 277 + 777 = 1503 Duger!
 

Uppg. 8:
När en bonde skulle programmera sitt fyrsiffriga kodlås till ett av uthusen, bestämde han att den tredje siffran skulle vara 4 samt att alla fyra siffrorna skulle vara olika. Dessutom skulle siffrorna bilda ett tal, som var jämnt delbart med 45.
Hur många olika kombinationer fanns det då?		   Svar: 14 sätt 
Lösning:
Jämnt delbart med 45 innebär att
● sista siffran är 0 eller 5
● siffersumman är delbar med 9.
   Det betyder i det här fallet att siffersumman
   är 9 eller 18.

0945    1845    2340    2745    3240    3645
5940    6345    6840    7245    8145    8640
9045    9540
 

Tillbaka