Lätt:
Svar: 80 % (4/5)
Lösning:
För att få minst 100 kr mer än den andra, måste den enas
belopp vara minst 300 kr.
I fig. nedan visar den blå markeringen att Maria får minst 300 kr och den röda markeringen att Sofie får
minst 300 kr.
Med andra ord är 4/5 färgmarkerat, dvs. 80%.
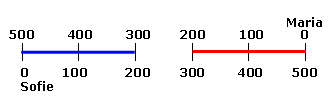
Svår:
Svar: 25% (1/4)
Lösning:

En lösning utan att använda integraler, skulle kunna se ut så här:
Antag att pekpinnen är 1 (m) och att pekpinnen
brutits av vid x resp. y, där y > x (se fig.)
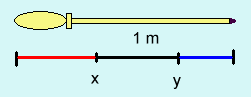
Delarnas längd är då x m (röd), (y-x) m (svart) och (1-y) m
(blå).
Om delarna skall bilda en triangel, måste den sammanlagda
längden av två delar vara större än den tredje delen
(triangelolikheten).
Vi måste därför kräva att varje del är <0,5 m, dvs. att
x<0,5 och y>0,5
Sannolikheten för att det skall inträffa är 1/2 (jämför att
kasta två mynt och få en krona och en klave).
Avståndet y-x kan ligga mellan 0 och 1, men för att
triangelolikheten skall gälla, måste y-x<0,5. Sannolikheten
for att det skall inträffa är 1/2.
Multiplikationsprincipen ger 1/2*1/2=1/4
BASIC-programmet
nedan stöder resultatet ovan:
10 FOR A =1 TO 10000
20 RANDOMIZE TIMER
30 X=RND(0)
40 RANDOMIZE TIMER
50 Y=RND(0)
60 IF X>Y THEN LET X1=X:X=Y:Y=X1:REM RAD 70, 80 OCH 90
FÖRUTSÄTTER ATT Y>X
70 IF 1-Y>Y THEN 110:REM TRIANGELOLIKHETEN UPPFYLLS EJ
80 IF 2*Y-2*X>1 THEN 110:REM TRIANGELOLIKHETEN UPPFYLLS
EJ
90 IF 2*X>1 THEN 110:TRIANGELOLIKHETEN UPPFYLLS EJ
100 GOSUB 140
110 NEXT A
120 PRINT 100*S/(A-1);"%"
130 END
140 S=S+1
150 RETURN |
|
|