Uppg. 1:
Svar:
306
Lösning:
Antag, att det ursprungliga svaret är 10a + b (där b är
entalssiffran)
Antag att det "synliga" svaret är a.
Differensen är 276 men den kan också skrivas 10a + b - a
Ekv.: 10a + b - a = 276
9a + b = 276
9a måste vara 270. (Annars blir inte b en entalssiffra.) Då är b
= 6
a = 270/9
a = 30
Det ursprungliga svaret är 10 a + b = 300 + 6 = 306 |
Uppg. 2:
Svar:
Sofie hann skriva 69 tal. Det tal som
inte syntes är 7.
Lösning:
I en talföljd 1, 2, 3, 4, 5 .... är medelvärdet och
medianvärdet lika stort.
Eftersom medelvärdet av de återstående talen är 35
7/17
kan man dra två slutsatser:
1) Medianvärdet var ursprungligen ca 35.
Man kan därför dra slutsatsen att antalet tal, som Sofie hann
skriva, var ca 70.
2) Antalet återstående tal måste vara delbart med 17. Det tal som
ligger närmast 70 och är delbart med 17 är 68.
Antalet återstående tal är 68 st. Antalet tal, som Sofie
hann skriva, är därför 69.
Summan av de 69 talen kan beräknas med formeln för den
aritmetiska serien: n(n + 1)/2
69.70/2 = 2415
Summan av de kvarvarande 68 talen är 68 .
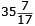 = 2408
= 2408
Det tal som inte syntes är 2415 - 2408 = 7 |
|