Månadens problem augusti 2024

Månadens problem
augusti 2024 (lösning)

Problem för hängmattan och badstranden del 2

KVADRATERNA

a) Svar: 14 kvadrater
Lösning: Kvadraten 3 x 3 rutor kan placeras på ett sätt
             Kvadraten 2 x 2 rutor kan placeras på 2 * 2 sätt = fyra sätt
             Kvadraten 1 x 1 ruta kan placeras på 3 * 3 sätt = nio sätt
             1 + 4 + 9 = 14
             (Matematiskt kan man också skriva det: 1² + 2² + 3² = 14)
b)

DET HEMLIGA TALET

a) Svar: 15 b) Svar: 21
Mönster: Summan av talen 1 - 5 är 15 och summan av talen 1 - 6 är 21.
Antag att vi t.ex. har talen A, B och C och lägger ihop A och B.
Då har vi två tal, (A och B) och C. När jag lägger ihop dem har jag A + B + C. Oberoende av hur många tal jag har från början, får jag till slut kvar ett tal, som är summan av alla de ursprungliga talen.
c) Svar: 120
Summan kan räknas ut med formeln n ^.(t₁ + t_n)/2 = 15(1 + 15)/2 = 120

REKTANGLARNA

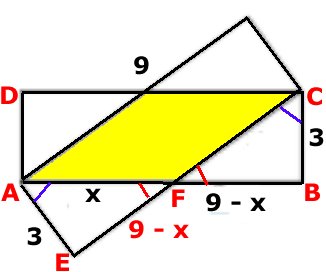
Svar: 15 cm²
Lösning:
Antag att AF är x cm och
FB (9 - x) cm
Av vinkelmarkeringarna framgår att trianglarna AEF och BCF är likformiga.
AE = BC => trianglarna också är kongruenta.
Då är EF = FB = (9 - x) cm.
Pythagoras sats på triangeln AEF:
3² + (9 - x)² = x²9 + 81 -18x + x² = x²18x = 90
x = 5

Arean av det gula området, som är en parallellogram (romb) =
basen ^. höjden = AF ^. BC =
5 ^. 3 cm² = 15 cm²

FAKULTET

n! = n³- n

Svar: n = 5
Lösning:
n! = n³- n                             Skriv om n! som n(n - 1)! och n³ - n som n(n² - 1)
n ^.(n - 1)! = n(n² - 1) Använd konjugatregeln på högra ledet.
n ^.(n - 1)(n - 2)! = n(n + 1)(n - 1)   Dividera båda leden med n(n - 1)
(n - 2)! = n + 1                                  Av vänsterledet framgår att n ≥ 3

n	(n - 2)!	n + 1	Kontroll
3	1! = 1	4	Stämmer inte
4	2! = 1^•2 = 2	5	Stämmer inte
5	3! = 1^•2 ^•3 = 6	6	Stämmer!
Den enda lösningen! (n - 2)! ökar allt snabbare, medan n + 1 endast ökar med 1, när n ökar med 1.

Den ursprungliga ekvationen
n! = 5! = 1 ^. 2 ^. 3 ^. 4 ^. 5 = 120
n³ - n = 5³ -5 = 120

beviset

Påst.:
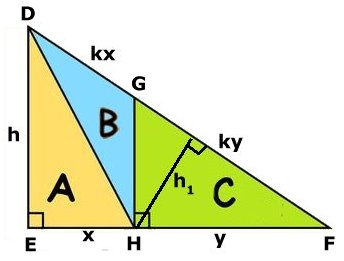
Bevis:
Ekv. 1:
A/(B + C) = x/y (1)

Arean A har samma höjd (h) som
arean B + C.
Då förhåller sig areorna som x/y

Ekv. 2:
På grund av likformighet kan
DG skrivas som kx och FG som ky.
Då gäller att
B/C = kx/ky => B/C = x/y (2)
B och C har samma höjd (h₁).
Då förhåller sig areorna som kx/ky = x/y

Ekv. (1) och (2) ger

V.S.B.
____