|
Månadens
problem |
Problem för hängmattan
och badstranden del
2 |
|
|
trolleri? |
|
 |
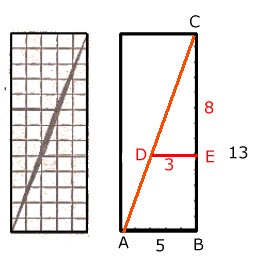Lösning: I figuren till vänster ser man att det blir en glipa mellan de fyra bitarna. Den motsvarar 1 cm2. AC är alltså inte en rät linje. Det betyder att triangeln CDE är inte likformig med triangeln CAB. Triangeln CDE: DE/CE = 3/8 = 0,375 Triangeln CAB: AB/CD = 5/13 ≈ |
|
kvadraten |
|
|
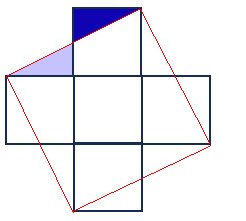
Lösning: De röda linjerna visar den stora kvadratens sidor. Gör så här: Klipp så att den mörkblå triangeln kan placeras på den ljusblå triangelns plats och fortsätt sedan på liknande sätt så att du får fram de övriga tre sidorna. |
 |
|
Tips: Om de små kvadraterna har sidan 1 längdenhet är deras sammanlagda area 5 areaenheter. Den stora kvadraten har då arean 5 areaenheter och sidan 
längdenheter. Med hjäp av Pythagoras sats ser man att den
röda kvadraten har sidan
längdenheter.____ |
____
|
|
kyssen |
|
|
Ett förslag till lösning: Fransmannen (motståndsman) njöt av situationen. Han var säker på att tysken aldrig skulle kunna lista ut att fransmannen hade kysst sin egen hand och därefter slagit till tysken. ________ |
|
|
sträckan cf |
|
|
Svar:
Sträckan CF är 3 cm. Lösning: Drag sträckan GK parallell med sidan AD och och sträckan HL parallell med sidan AB. Visa sedan att trianglarna KEG och LFH är likvinkliga och därmed likformiga. Eftersom sträckan GK är lika lång som sträckan HL, kan vi gå ett steg längre: De båda trianglarna KEG och LFH är kongruenta. Låt KE = x. Då är även LF = x. Låt CF = y Eftersom AB = BC får vi ekv. 4 + x + 6 = 7 + x + y y = 3 ____ |
 Extrauppgift: Svar: Kvadratens sida > 10 cm Lösning: x kan anta ett godtyckligt positivt värde. Om kvadratens sida är a, gäller att a >10 cm. |
|
den tankspridde bankkassören |
|
|
Svar: Checken löd
på 31 dollar och 63 cent Lösning: Antag att checken löd på x dollar och y cent. Skriv en ekvation där alla värden uttrycks i enheten cent. Checken: 100x + y Efter felväxling och tidningsköp: 100y + x - 5 Ekv.: 100y + x - 5 = 2(100x + y) 98y = 199x + 5 y = (199x + 5)/98 Denna diofantiska ekvation har oändligt många lösningar. Lösningen med de lägsta värdena är x = 31 $ och y = 63 cent Övriga lösningar, t.ex. x = 129 och y = 262 duger inte, eftersom antalet cent ska vara mindre än 100. En elegantare lösning På checken stod det x dollar och y cent Sedan mr. Black köpt tidningen har han kvar 2x dollar och 2y cent. De växelmynt som han har kvar är x - 5 cent. y < 100 Fall 1 y < 50 2x = y 2y = x - 5 Detta ekvationssystem saknar positiva heltalslösningar Fall 2 50 ≤ y < 100 Fördubbling av antalet cent på checken ger ytterligare 1 dollar Antalet cent är då 2y - 100 Jämför med ekvationssystemet i fall 1! 2x + 1 = y 2y - 100 = x - 5 Detta ekvationssystem har lösningen x = 31 $ y = 63 cent __ |
|