Uppg. 1:
Hotellrummet
Svar: Ingen krona har försvunnit!
Problemet är formulerat så att man ska luras att gör
den felaktiga additionen
87 + 2 = 89
I själva verket ska man ju resonera så här:
Männen betalade 87 kr.
Portiern behöll 85 kr och hisspojken stoppade 2 kr egen
ficka.
85 kr + 2 kr = 87 kr
|
Uppg. 2:
Svar: Fastighetsägaren hade rätt!
Lösning:
Muren har samma volym som om den hade varit horisontell.
Det framgår av fig. nedan.
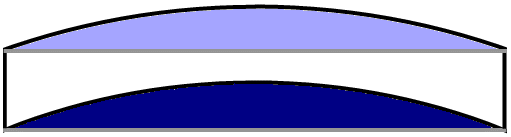
Om den övre ljusblå delen av muren ersätts av den mörkblå, får
man en horisontell mur med längden 20 m.
Källa: Heinrich Hemme: Die Hölle der Zahlen (som i sin tur har
hämtat uppgiften från Henry Ernest Dudeney) |
|
Uppg. 3: Schackbrädet och vetekornen
Svar:
Härskaren blev grundlurad!
Antalet vetekorn blir astronomiskt stort,
264 - 1 »
1,8 . 219 st (18 triljoner)
Lösning:
Vi försöker hitta en formel för totala antalet vetekorn:
3 rutor: 1 + 2 + 4 = 7 = 23
- 1
4 rutor: 1 + 2 + 4 + 8 = 15
= 24 - 1
5 rutor: 1 + 2 + 4 + 8 + 16
= 31 = 25 - 1
osv.
64 rutor: 264
- 1
Generellt kan antalet korn skrivas 2n - 1, där
n är antalet schackrutor.
För att få en uppfattning om denna oerhört stora mängd vetekorn,
kan vi jämföra med den nuvarande årsproduktionen
av vete, som är ca 600 milj. ton = 6 .
108 ton (enligt FAO 2007).
Om vi antar att ett vetekorn väger
0,05 g = 5.10-2 g = 5.10-5 kg =
5.10-8
ton, kommer alla vetekornen att väga 1,8 .
219 . 5.10-8 ton
»
9. 1011 ton, dvs. oerhört mycket mer
än årsproduktionen av vete!! (Ca 1500 gånger så mycket som
årsproduktionen.)
Anm.:
Det är möjligt att antagandet om att ett vetekorn väger 0,05 g
(enligt
Wikipedia) avviker en del från det korrekta värdet
(fuktighetshalten inverkar naturligtvis), men under alla
omständigheter torde förhållandet mellan vikten av vetekornen på
schackbrädet och vikten av årsproduktionen ligga i intervallet
1000 - 3000. |
|