|
Matematikens hopp
 |
Uppgift 1:
Svar:
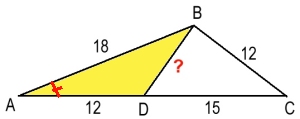
Sträckan BD är 8 cm.
Lösning:
Sträckan BD kan beräknas med hjälp av cosinussatsen, men
ett enklare sätt är att använda likformighet.
|
 |
|
I den här uppgiften är vinkeln
mellan de två största sidorna i trianglarna ABC och ABD gemensam.
Förhållandet mellan de två största sidorna i respektive triangel är
lika stort.
AB/AD = 18/12 = 3/2 och AC/AB = 27/18 = 3/2
Då är trianglarna ADB och ABC likformiga.
Likformighet ger:
BD/12 = 18/27
BD = 8
Anm.: Denna uppgift var föreslagen som en svår
uppgift för högstadieelever, men refuserades eftersom
högstadieelever inte kan cosinussatsen. Ridå! |
Uppgift 2:
Svar:
45°
Lösning:
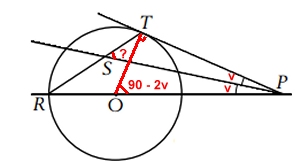
Vinkeln TPS = vinkeln SPR = v
Radien OT är vinkelrät mot tangenten TP.
Då är vinkeln TOP 90 - 2v
(Vinkelsumman i triangeln OPT är 180o)
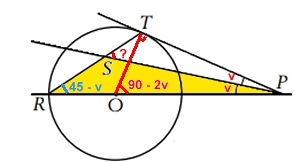
Vinkeln TRP = 45 - v (Hälften så stor som vinkeln TOP enligt
randvinkelsatsen).
Vinkeln TSP är yttervinkel till den gula triangeln SRP.
Enligt yttervinkelsatsen
är vinkeln TSP = 45 - v + v = 45
OBS! Storleken av vinkeln TSP påverkas inte av
punkten P:s läge!
Alternativ lösning:
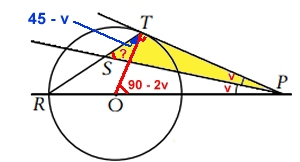
Triangeln ORT är likbent.
Vinkeln OTR är 45 - v
(Hälften av 90 - 2v enligt yttervinkelsatsen.)
Vinkelsumman i triangeln PST ger:
Vinkeln TSP = 180 - (45-v) - 90 -v = 45
|
  |