Svar: Sträckan AE är 65 m
Lösning:
Antag att det finns n blå sträckor.
Då finns det (n - 1) röda sträckor.
Pelle P. har föreslagit följande lösning:
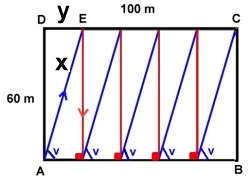
Sträckan AE är x m och sträckan DE y m.
602 + y2 = x2 (1)
n . y = 100 (2)
n . x + 60(n - 1) = 440 (3)
Efter förenkling blir (3) n . x + 60n= 500 (4)
(2) kan skrivas n = 100/y
(4) kan skrivas n = 500/(x + 60)
Då är 100/y = 500/(x + 60)
Efter förenkling får man x = 5y - 60
x = 5y - 60 insatt i (1) ger
602 + y2 = (5y - 60)2
Efter förenkling:
24y2 - 600y = 0
24y(y - 25) = 0
(y1 = 0)
y2 = 25
Pytagoras sats på triangeln ADE ger
x = 65
Anm.:
Professor Kalkyl går hela tiden längs hypotenusan och den längsta
kateten i en s.k. indisk triangel.