Metod Med logik kan man lösa de

Tillbaka till sudokusidan

Metod
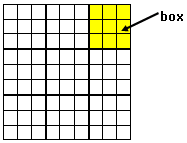
Ett sudoku består av 9x9 rutor. Kvadrater med 3x3 rutor bildar en box.

Med logik kan man lösa de flesta Sudokun. Därför ska man använda "Trial and error" först när alla andra möjligheter är uttömda.
Här följer några förslag till metoder:

Metod 1: Jämför raderna i en hel boxgrupp

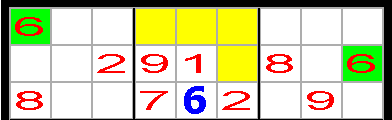
Sexorna i de gröna rutorna i den översta boxgruppen blockerar de gula rutorna. I den mellersta boxen finns det därför bara en möjlig ruta för den blå sexan.
Anm.: På motsvarande sätt kan man naturligtvis jämföra de lodräta raderna i en lodrät boxgrupp.

Metod 2: Jämför en vågrät och en lodrät boxgrupp

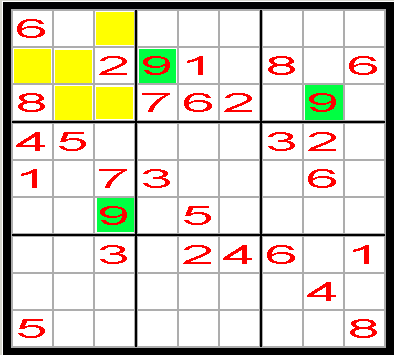
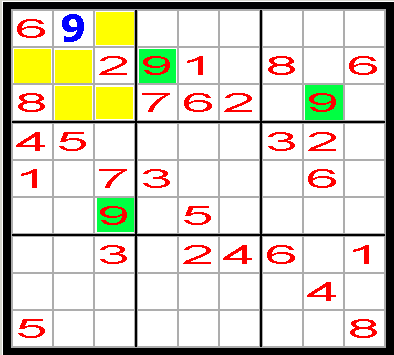
Vi jämför den översta boxgruppen med den lodräta boxgruppen längst till vänster. Niorna i de gröna fälten blockerar de gula rutorna i boxen längst upp till vänster. Därför finns det bara en ruta, där vi kan placera den blå nian (se fig. nedan).

Metod 3: Kontrollera vilka siffror som saknas i raden/boxen och undersök om man kan bestämma vilken siffra som skall finnas i en viss ruta.

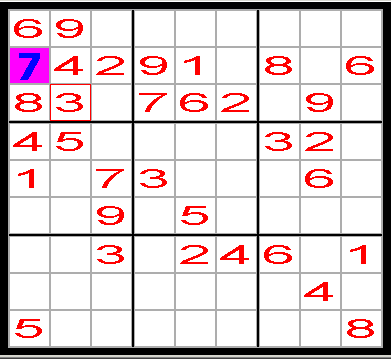
Vilken siffra skall finnas i den violetta rutan?
I den översta vänstra boxen finns siffrorna 2, 3, 4, 6, 8, 9.
Siffrorna 1, 5 och 7 saknas alltså, men 1 och 5 finns ju i den första lodräta raden.
Därför blir slutsatsen att siffran 7 skall placeras i den violetta rutan.
Anm.: Naturligtvis hade det i det här fallet också varit möjligt att tillämpa metod 2.

När man fått ut så många siffror som möjligt med hjälp av metod 1-3 är det dags för en ännu effektivare metod!

Metod 4: Fyll i alla tänkbara siffror som kan finnas i de återstående rutorna.

a) bundna par

Om siffrorna i två rutor i en rad eller en box stämmer överens och dessa rutor endast innehåller två siffror, säger vi att de bildar ett bundet par.
I exemplet ovan utgör siffrorna 3 och 8 i de gula rutorna ett bundet par. Siffrorna 3 och 8 ska alltså placeras i i ruta nr 5 och ruta nr 8, men vi vet inte på vilket sätt. Däremot vet vi att siffrorna 3 och 8 inte kan förekomma i någon annan ruta på den här raden. Vi kan därför stryka trean i ruta nr 1. Därefter kan vi stryka åttan och ettan i ruta nr 7 (se fig. nedan).

b) bundna tripplar
Om det visar sig, när man fyllt i alla tänkbara siffror i rutorna, att det totalt sett finns endast tre olika slags siffror i tre av rutorna i en rad eller box, säger man att de tre rutorna innehåller en bunden trippel. Då kan ingen annan ruta i raden resp. boxen innehålla någon av dessa siffror! Observera att alla tre siffrorna inte behöver finnas i alla tre rutorna.

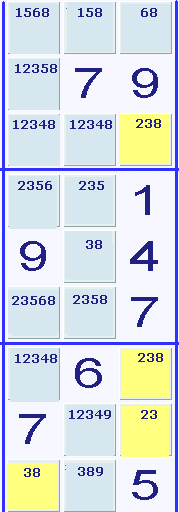I den tredje lodräta raden bildar siffrorna 2, 3 och 8 en bunden trippel i de gula rutorna: 238, 238 och 23. Då kan inte någon av dessa siffror förekomma i någon annan ruta i den tredje lodräta raden. Därför stryker vi åttan i den första rutan i den tredje lodräta raden. Sedan kan vi också stryka sexan i första rutan i den översta boxen (se fig. till höger).

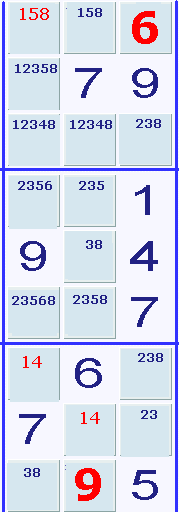
I den nedersta boxen har vi ytterligare en bunden trippel i de gula rutorna: 238, 23 och 38. I den åttonde rutan i boxen plockar vi bort siffrorna 3 och 8. Då återstår en nia. I den första rutan stryker vi siffrorna 2, 3 och 8 och i den femte rutan stryker vi siffrorna 2, 3 och 9 (se fig. till höger).
Anm.: De här två exemplen visar bundna tripplar i en lodrät rad resp. i en box. Givetvis kan tripplar också förekomma i en vågrät rad.

c) Bundna kvadruplar

I de gula rutorna bildar siffrorna 1, 5, 6 och 9 en bunden kvadrupel. Dessa fyra siffror kan då inte finnas i några andra rutor i den här raden. När vi stryker siffran 5 i ruta nr 4 återstår bara en trea! I ruta nr 1 kan vi stryka siffrorna 1 och 5 och dessutom siffran 3. I ruta nr 7 kan vi stryka siffran 3.

Anm.: Samma resonemang kan naturligtvis föras, om vi upptäcker en bunden kvadrupel i en lodrät rad eller i en box.

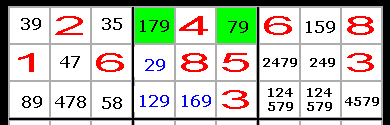
Metod 5: Jämför en rad och en box

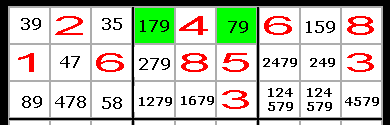
I den första raden finns siffran 7 endast i den mellersta boxen (de gröna rutorna).
Eftersom sjuan måste finnas i någon av dessa rutor, kan vi stryka övriga sjuor i den mellersta boxen. (Se fig. nedan)

OBS! Så fort man gör en förändring i någon ruta, kan förutsättningarna ändras för de andra rutorna!
Därför är det viktigt att man efter varje förändring kollar, om siffror i ytterligare någon ruta kan strykas.

Övningsexempel:
Tillämpa någon/några av metoderna 1-5

Ex. 1:	Ex 2:
Lösning:	Lösning:

Överst på sidan

Lösning till exempel 1:

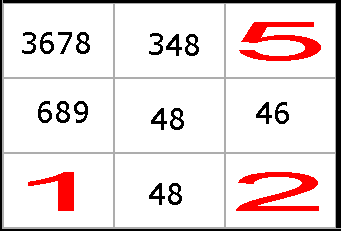
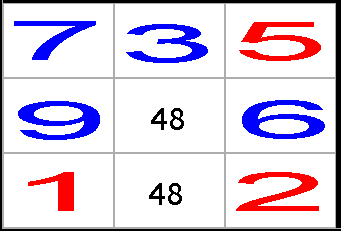
Man kan utnyttja att det finns en bunden trippel (348, 48 och 48) men i det här fallet är det enklare att undersöka om det finns rutor i boxen, där man direkt kan bestämma siffran:
1) Första rutan är den enda i boxen som innehåller en sjua.
2) Första rutan på den andra vågräta raden är den enda i boxen som innehåller en nia.
3) Eftersom vi har eliminerat sexan i den första rutan, är det endast den tredje rutan på den andra vågräta raden som innehåller en sexa.

Tillbaka till exempel 1 Överst på sidan

Lösning till exempel 2:

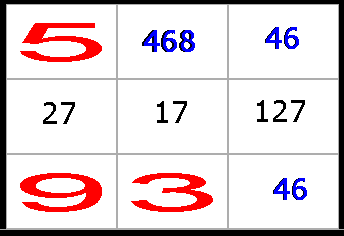
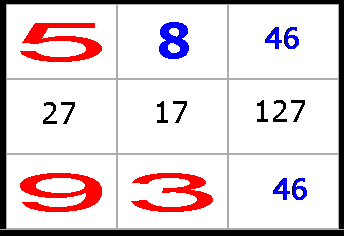
1) I boxen finns det en bunden trippel (27, 17, 127). Därför kan vi stryka siffrorna 1, 2 och 7 i övriga rutor i boxen.
2) Nu har vi fått ett bundet par (46, 46). Vi kan därför eliminera siffrorna fyra och sex i den andra rutan på den första vågräta raden, så att endast siffran 8 återstår.
Anm.: Givetvis ska vi sedan undersöka om sudokut i övrigt har påverkats av förändringarna ovan.

Tillbaka till exempel 2 Överst på sidan Tillbaka till sudokusidan

	I den tredje lodräta raden bildar siffrorna 2, 3 och 8 en bunden trippel i de gula rutorna: 238, 238 och 23. Då kan inte någon av dessa siffror förekomma i någon annan ruta i den tredje lodräta raden. Därför stryker vi åttan i den första rutan i den tredje lodräta raden. Sedan kan vi också stryka sexan i första rutan i den översta boxen (se fig. till höger). I den nedersta boxen har vi ytterligare en bunden trippel i de gula rutorna: 238, 23 och 38. I den åttonde rutan i boxen plockar vi bort siffrorna 3 och 8. Då återstår en nia. I den första rutan stryker vi siffrorna 2, 3 och 8 och i den femte rutan stryker vi siffrorna 2, 3 och 9 (se fig. till höger). Anm.: De här två exemplen visar bundna tripplar i en lodrät rad resp. i en box. Givetvis kan tripplar också förekomma i en vågrät rad.
c) Bundna kvadruplar I de gula rutorna bildar siffrorna 1, 5, 6 och 9 en bunden kvadrupel. Dessa fyra siffror kan då inte finnas i några andra rutor i den här raden. När vi stryker siffran 5 i ruta nr 4 återstår bara en trea! I ruta nr 1 kan vi stryka siffrorna 1 och 5 och dessutom siffran 3. I ruta nr 7 kan vi stryka siffran 3. Anm.: Samma resonemang kan naturligtvis föras, om vi upptäcker en bunden kvadrupel i en lodrät rad eller i en box.