Material:
Stort linjerat papper
tändsticka
|
1.
2.
3.
|
Gör så här:
Använd ett stort papper
(gärna 1 m x 1 m)
Rita parallella linjer.
Avståndet mellan dem skall vara lika stort som längden av den
tändsticka, som skall användas.
Kasta tändstickan så slumpmässigt som möjligt med avseende på
a) var tändstickan hamnar på papperet.
b) vinkeln mellan tändstickan och de parallella linjerna.
Notera totala antalet kast resp. skärningar.
Multiplicera totala antalet kast med 2 och dividera sedan med antalet
kast, där tändstickan skär en linje, för att få ett
närmevärde på
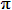 . .
Anm.:
1. Det här sättet att bestämma
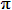 upptäcktes av den franske vetenskapsmannen greve Buffon på 1700-talet.
Den italienske matematikern Lazzerini fick fram närmevärdet 3,1415929
(den sjunde(!) decimal är felaktig) efter 3408 kast. Imponerande, men man
måste onekligen fråga sig varför han valde att göra just 3408
kast.
upptäcktes av den franske vetenskapsmannen greve Buffon på 1700-talet.
Den italienske matematikern Lazzerini fick fram närmevärdet 3,1415929
(den sjunde(!) decimal är felaktig) efter 3408 kast. Imponerande, men man
måste onekligen fråga sig varför han valde att göra just 3408
kast.
2. Tycker du att det verkar jobbigt att göra så många kast?
I så fall kan du testa simuleringar på nätet:
Buffon's Needle,
MSTE, University of Illinois
Välj antal simuleringar genom att
klicka på något av alternativen nedan.
Du hittar dem i slutet av
webbsidan.

Teori:
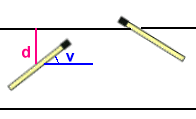
Två faktorer är avgörande för om stickan skär linjen:
a) avståndet d från stickans
mittpunkt till närmaste linje.
b) vinkeln v (i radianer) mellan
linjen och stickan eller dess förlängning.
Låt stickans längd vara 1 längdenhet
Slutsats: Stickan skär linjen, om 1/2*sinv > d
I fig. till höger representerar det gröna fältet de gånger stickan
skär en linje, medan rektangeln representerar
samtliga kast.
Sannolikheten för skärning av en linje är lika med förhållandet
mellan det gröna områdets area och rektangelns area.
Gröna området:
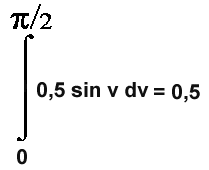
Rektangeln:
0,5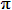 /2 /2
P(skärning) =
0,5/(0,5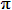 /2)
= 2/ /2)
= 2/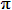
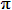 = 2*A/B
= 2*A/B
A= totala antalet kast och B =
antalet skärningar mellan tändstickan och linjerna. |
 -
laborationer
-
laborationer