Magiska kvadrater

Magiska kvadrater

Definitioner	Udda ordning	Jämn ordning	Upp och nervänd kvadrat
Benjamin Franklin	Djävulskvadrater		Ett shownummer

Tillbaka till Klurigt

Källor:
Carl-Otto Johansen: Magiska tal (Forum 1966)
Artur Benjamin/Michael Shermer: Secrets of Mental Math (Three Rivers Press 2006)
Wikipedia


Definitioner:
Def. 1:	I en magisk kvadrat får man samma resultat om man summerar talen i en vågrät eller lodrät rad eller längs en av diagonalerna.
Def. 2:	En magisk kvadrat av ordning n är en kvadrat bestående av n² rutor.

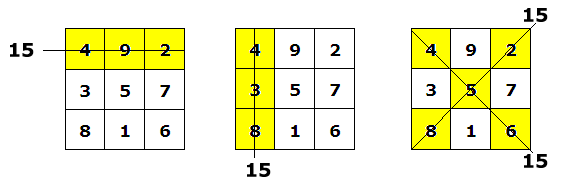
Def. 3:

I en kvadrat med n² rutor, där de naturliga talen 1 till n²placeras ut, är summan av talen i varje rad (n³ + n)/2
Ex.: I kvadraten ovan är n = 3 (n³ + n)/2 = (27 + 3)/2 = 15

Def. 4:

I en kvadrat med n² rutor, där de naturliga talen 1 till n²placeras ut, och n är ett udda tal gäller följande:
Talet i mittenrutan är (1 + n²)/2
Ex: I kvadraten ovan medför det att (1 + n²)/2 = (1 + 9)/2 = 5

Uppg.:
a) Hur stor är summan av talen i varje rad i en kvadrat av femte ordningen (5² rutor)?
Svar: n = 5 (n³ + n)/2 = (125 + 5)/2 = 65
b) Vilket tal ska placera i mittenrutan?
Svar: (1 + n²)/2 = (1 + 25)/2 = 13

Tillbaka

Magiska kvadrater av udda ordning

Tredje ordningen
I en kvadrat av tredje ordningen är siffran i mittenrutan en femma (def. 4)
I de fyra hörnen finns de jämna talen 2, 4, 6 och 8.

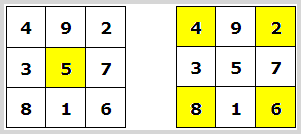
Kuriosa: 492² + 357² + 816² = 294² + 753² + 618²
438² + 951² + 276² = 834² + 159² + 672²

Femte ordningen
I en kvadrat av femte ordningen är siffran i mittenrutan (1 + n²)/2 = (1 + 25)/2 = 13
En generell metod för att placera ut talen i en magisk kvadrat av udda ordning ser ut så här:

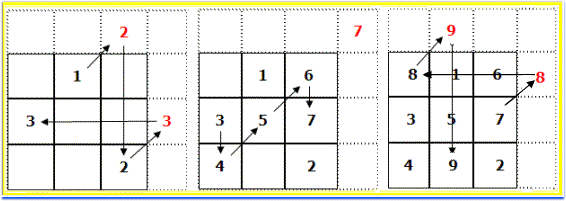
1)	Börja med en etta mitt i den översta raden.
2)	Nästa tal ska placeras snett uppåt höger.
3)	Kommer man utanför kvadraten, fortsätter man istället i andra änden av raden eller kolumnen. OBS! Om man kommer till en ruta i diagonalens förlängning (jfr den mellersta fig. ovan), kan man ju inte fortsätta till andra änden av raden/kolumnen. Istället placeras siffran direkt under föregående siffra.
4)	Om man kommer till en upptagen ruta, placeras siffran istället direkt under föregående siffra.

Uppg.: Konstruera en kvadrat av femte ordningen.
Lösning

Tillbaka

Magiska kvadrater av jämn ordning

Fjärde ordningen
Det är enkelt att konstruera en magisk kvadrat av fjärde ordningen.
1) Skriv upp talen 1-16 i ordningsföljd i en kvadrat.
2) Kasta om talen längs diagonalerna. (Se fig. nedan)

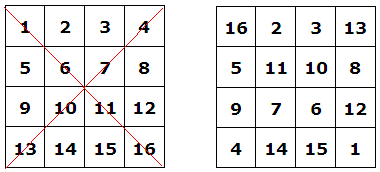
OBS! Förutom att summan av talen i varje vågrät rad, varje lodrät rad och varje diagonal är 34, gäller samma sak för talen i de färgade områdena i fig. nedan.

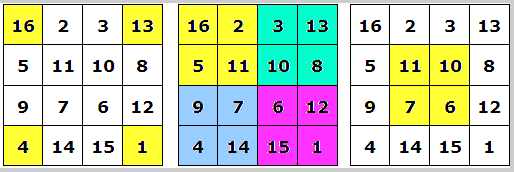
I sitt kopparstick Melankolin (Melancolia I) har den tyske konstnären Albrecht Dürer en magisk kvadrat, där de lodräta raderna 2 och 3 är omkastade. (Se fig. nedan).

OBS! Kopparstick tillverkades 1514 (de två mellersta rutorna i nedersta raden). Kuriosa: Liksom för kvadraten ovan gäller att summan av kvadraterna på talen i de två diagonalerna är lika stor som summan av kvadraterna på resten av talen, och detsamma gäller deras kuber.
Denna kvadrat finns med i Dan Browns bok "Den förlorade symbolen" (2009).

Tillbaka

Magisk kvadrat även när den vänds upp och ner

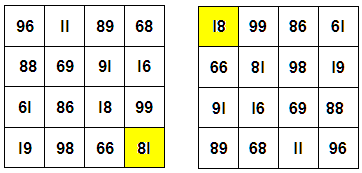
Tillbaka

Benjamin Franklins magiska kvadrat

Benjamin Franklin var en mångsidig person, till största delen självlärd. Historien om hur han gjorde livsfarliga experiment genom att sända upp en drake i ett åskmoln så att gnistor slog ut från snöret är välkänd. Senare uppfann han åskledaren. Han var också politiker, känd för sin medverkan vid USA:s självständighetsförklaring 1776.
Benjamin Franklin har konstruerat flera ovanliga magiska kvadrater. Här är ett exempel på en kvadrat av åttonde ordningen:
1) Summan av talen i alla vågräta och lodräta rader samt längs diagonalerna är 260.
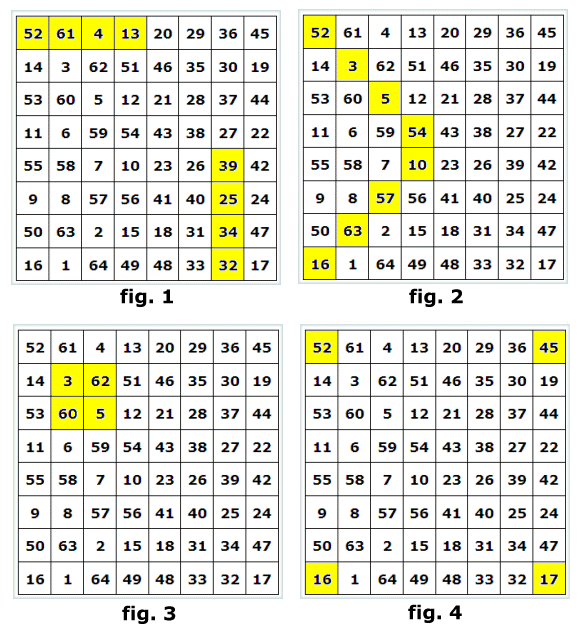
2) Summan av talen i alla halva vågräta och lodräta rader är 130 (fig. 1 nedan).
3) Summan av talen i en knäckt diagonal är 260 (fig. 2).
4) Välj vilken kvadrat som helst med 2x2 rutor. Summan av talen är alltid 130! (fig. 3)
5) Summan av de fyra hörntalen är 130 (fig. 4).
6) Det finns många andra sätt att få summan 130 eller 260.

Uppg.: Hitta ytterligare ett sätt att få summan 130.
Ledning

Uppg.: Hitta ytterligare något sätt att få summan 260.

Tillbaka

Benjamin Franklins magiska kvadrat spelar en avgörande roll i Dan Browns bok "Den förlorade symbolen" (2009).

Djävulskvadrater

En kvadrat av fjärde ordningen finns i Khajuraho i Indien (från 1000- eller 1100-talet)
Den är en s.k. djävulskvadrat.

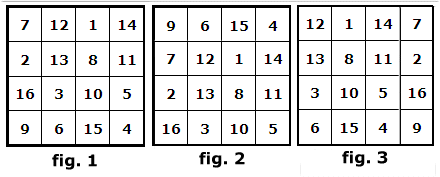
1)	Precis som en vanlig kvadrat av fjärde ordningen är summan av talen (radvis och diagonalt) 34. Se fig. 1.
2)	En djävulskvadrat förblir en djävulskvadrat om en vågrät rad flyttas från nederkanten till överkanten eller om en lodrät rad flyttas från den ena kanten till den andra. Se fig. 2 och 3.
3)	Även rotationer och spegelvändningar ger fortfarande en djävulskvadrat.
4)	Om vi lägger samman ett stort antal likadana djävulskvadrater, kan vi välja vilken grupp av 4x4 rutor som helst. Den är alltid en djävulskvadrat.

Tillbaka

Magiska kvadrater som ett shownummer!

Arthur Benjamin beskriver i sin bok "Secrets of Mental Math" följande trick:

1)	Först visar jag den magiska kvadraten och förklarar vilka egenskaper den har.

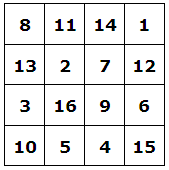Summan av talen i varje vågrät rad, varje lodrät rad och varje diagonal är 34.

2)	Sedan ber jag någon i publiken ange ett större tal än 34.
3)	Låt oss anta att personen säger talet 67.
4)	Snabbt ritar jag upp följande magiska kvadrat:

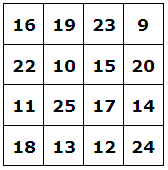En kontroll visar, att summan av talen i varje vågrät rad, varje lodrät rad och varje diagonal är 67.

5)	Jag påpekar dessutom att summan av talen i de fyra hörnen är 67.
6)	Om man väljer en kvadrat med 2x2 rutor i hörnen eller i centrum av den magiska kvadraten är summan av talen 67! Anm.: Om summan är ett jämnt tal, kan man välja vilken kvadrat som helst med 2x2 rutor.

Metod:
1)	Utgå från den ursprungliga kvadraten.
2)	Subtrahera det angivna talet med 34 (67 - 34 = 33)
3)	Dividera detta svar med 4 ( 33/4 = 8 rest 1). Det ger oss två "magiska" tal, 8 och 9.
4)	Titta så omärkligt som möjligt på den ursprungliga kvadraten.
5)	Öka talen med det "magiska" talet 8 utom i de rutor där talen 13, 14, 15 och 16 finns. Där ökar du talen med det "magiska" talet 9. Anm.: Om du i punkt 3 inte får någon rest, ska alla talen i kvadraten ökas med samma "magiska" tal.

OBS!

Inget av talen 13, 14, 15 och 16 ligger i samma rad eller samma kolumn!
Talen 15 och 16 tillhör var sin diagonal.

Uppg.: Vilka blir de "magiska talen" om personen istället hade sagt talet 85.
Svar: (85 - 34 = 51 51/4 = 12 rest 3) De "magiska" talen blir 12 och 15.

Tillbaka

Kvadrat av femte ordningen

Tillbaka

Ledning: Välj fyra rutor, som är symmetriskt placerade

Tillbaka