Kuriosa




¨

De gamla grekerna använde aldrig för att beteckna förhållandet mellan cirkelns omkrets och diameter.
Inte förrän på 1700-talet definierades som kvoten av cirkelns omkrets och diameter. Bland ledande matematiker var Euler först att använda i denna betydelse. 
¨ Naturligtvis finns det inget återkommande regelbundet mönster bland :s decimaler, eftersom är ett irrationellt tal. Ändå finns det goda utsikter för dig att hitta ditt födelsedatum eller ditt telefonnummer bland :s decimaler.
På http://gryphon.ccs.brandeis.edu/~grath/attractions/gpi kan du kolla detta.
¨ Martin Gardner, känd för sina böcker med matematiska problem, har påpekat att man faktiskt kan få fram ett närmevärde för med fyra decimaler genom att utnyttja det engelska alfabetet:
Skriv bokstäverna i ordning i en cirkel och ta sedan bara hänsyn till antalet bokstäver i varje grupp som inte innehåller symmetriska bokstäver. Starta med bokstaven J.
J K L M N O P Q R S T U V W X Y Z A B C D E F G H I
Resultatet blir som synes 3 1 4 1 6 (pi = 3,14159…)
¨ År 1873 kungjorde engelsmannen W. Shanks att han hade beräknat 707 decimaler, något som väckte stor uppmärksamhet i matematiska kretsar. Shanks var också mycket stolt över sin prestation, och i sitt testamente begärde han att alla decimalerna skulle huggas in på hans gravsten. Så skedde också, men 1945 visade en matematiker att de 180 sista decimalerna var felaktiga! Det som skulle ha varit ett monument över en storslagen prestation är nu istället ett bevis för en av de mera kända vetenskapliga fadäserna.
¨ Eulers formel:
Ett oväntat resultat! e är ett irrationellt tal, i betyder 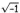  och p är ett irrationellt och transcendent tal. Ändå blir högerledet ett negativt heltal.
¨ Srinivasa Ramanujan, föddes i en fattig familj i södra Indien år 1887. Han hade ingen egentlig matematisk skolning, men hans intuition var fenomenal. År 1913 skickade han sina arbeten till tre engelska matematiker. En av dem, G.H. Hardy, blev så imponerad att han inbjöd Ramanujan att komma till England. På så sätt blev dennes ekvationer kända.
Tyvärr blev Ramanujan kroniskt sjuk* kort efter sin ankomst till England. Han dog 1919 endast 32 år gammal.
I mitten av 80-talet utvecklade två matematiker - på grundval av studier av Ramanujans formler - en mycket kraftfull ekvation för beräkning av .
Idag arbetar fortfarande matematiker med att utveckla algoritmer för datorberäkningar med utgångspunkt från hans ekvationer.
*När G.H. Hardy vid ett tillfälle besökte honom på sjukhuset, nämnde han att taxin hade haft numret 1729. "Vilket intressant tal utropade Ramanujan blixtsnabbt. 1729 är det minsta tal som kan skrivas som summan av två kubtal på två olika sätt."
13 + 123 = 1729 och 93 + 103 = 1729.
Nästa tal är 4104 (23 + 163 och  93 + 153)
¨ Pi-dagen
Den 14 mars varje år firas Pi-dagen, efter det angolsaxiska sättet att skriva datumet, 3.14. 
Den 14 augusti, tyvärr inte den 14 mars (-: , 2012 uppgick den amerikanska befolkningen till 314 159 265 invånare, dvs. 100 miljoner gånger närmevärdet för pi med åtta decimaler.

I följande historia har dock fysikern och ingenjören vissa synpunkter på betydelsen av pi.
A mathematician, a physicist, and an engineer are all given identical rubber balls and told to find the volume. They are given anything they want to measure it, and have all the time they need.
The mathematician pulls out a measuring tape and records the circumference. He then divides by two times pi to get the radius, cubes that, multiplies by pi again, and then multiplies by four-thirds and thereby calculates the volume.

The physicist gets a bucket of water, places 1.00000 gallons of water in the bucket, drops in the ball, and measures the displacement to six significant figures.

And the engineer? He writes down the serial number of the ball, and looks it up.