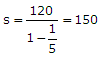|
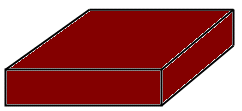
En kaka är chokladglaserad
på alla sidoytor utom den kvadratiska botten. Tomtemor vill skära kakan
i fem bitar så att var och en av de fem medlemmarna i familjen får samma
mängd kaka och lika mycket glasyr. Alla snitt ska vara vinkelräta mot
kakans översida och varje tomte ska få sin del som en
sammanhängande bit.
Hur ska det gå till?
|
 |
|
När en professor i
matematik (Nämnaren 2001) ska lösa det här problemet föreslår han
följande strategi:
Dela in randen (av ovansidan min anm.) i 5 lika delar och
”fortsätt sedan dessa inåt” på ett sådant sätt att motsvarande delar får rätt
area. |
|
Den metoden tillämpas i det första
exemplet. |
 |
|
I det
andra exemplet är målsättningen att få så många
symmetriska områden som möjligt.
Följande instruktioner ges:
|
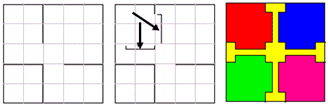 |
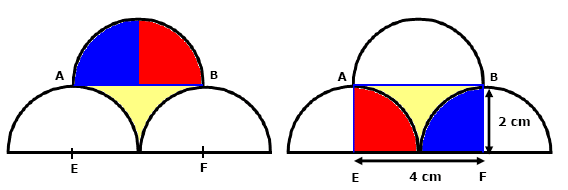
| Börja med att markera en kvadratisk bit kring varje hörn med
sidlängd 2 och area 4. Utöka sedan varje hörnbit så att arean
blir 4+1, t.ex. genom att "tjocka" 3 längdenheter med 1/3. Se
pilarna |
|
| Komm.:
Strategin att dela randen i fem delar är korrekt, men sedan hittar inte
professorn den teoretiskt sett enklaste lösningen. De praktiska
problemen, som han råkar ut för, när han ska dela kakan, ska vi bara inte tala om! |
|
Så här tycker jag att lösningen bör se ut:
På bilden till höger är ovansidans rand indelad i fem lika stora delar.
Delningslinjerna sammanstrålar i ovansidans (kvadratens) mittpunkt.
Antagande:
Kvadratens sida är a cm och randen till det gula området är (x + y)
cm.
Påst.:
Varje del utgör då en en femtedel av hela kakan.
Bevis:
Kvadratens omkrets är 4a cm.
Då är (x + y) = 4a/5 (1)
Kvadratens area är a2 cm2. Det gäller därför
att bevisa att det gula områdets area är a2/5 cm2.
|
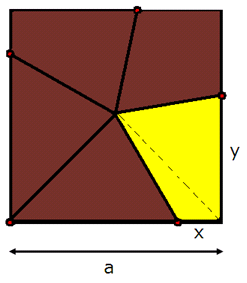 |
Det gula området kan delas upp i två
trianglar
Deras sammanlagda area är
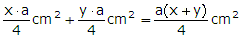
Men (x + y) = 4a/5 enligt ekv. (1)
|
Arean kan
därför skrivas
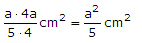
V.S.B. |
|
Professorns kommentar till
min lösning: Jag tror du har helt rätt, jag hade helt enkelt inte tänkt
på detta. Vad jag förstår funkar din lösning lika bra för en godtycklig
regelbunden m-hörning och ett godtyckligt antal bitar x.
|
Exempel 4: Tåget
|
Ett tåg består av ett lok och fem vagnar
(A, B, C, D och E).
På hur många sätt kan vagnarna ordnas så att vagn A kommer närmare loket
än vagn B kommer?
 |
Metod 1:
Vi utreder olika alternativ:
|
A |
|
|
|
|
|
Övriga fyra vagnar kan placeras på
4! = 1.2.3.4 = 24 sätt. |
| |
A |
|
|
|
På plats nr 1 (röda fältet) kan
man välja mellan tre alternativ (C, D och E).
På de tre platserna efter vagn A kan sedan återstående vagnar
placeras på 3! sätt = 6 sätt.
Totalt: 3 . 6 sätt = 18 sätt. |
|
| |
|
A |
|
|
|
Man undersöker på hur många sätt
två av vagnarna C, D och E kan placeras på plats nr 1 och plats
nr 2. Man inser lätt att det finns sex möjligheter (CD,
DC, CE, EC, DE och ED). På de två sista platserna (svarta resp.
gröna fältet) kan B och den återstående vagnen placeras på
två sätt. Totalt: 6 . 2 sätt = 12 sätt.
|
|
| |
|
|
A |
|
|
I det här fallet måste B
placeras på den sista platsen i tågsättet. Övriga tre
vagnar kan placeras på 3! sätt = 6 sätt. |
| |
|
|
|
A |
|
Naturligtvis ger detta
alternativ inga nya möjligheter. |
|
Sammanlagt: 60 sätt |
Metod 2:
Fem vagnar kan placeras på 5! sätt = 1.2.3.4.5
sätt = 120 sätt. I hälften av dessa fall kommer vagn A före vagn B.
|
Tillbaka
Exempel 5:
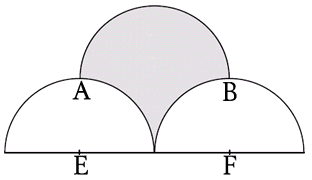
Cirklarna
|
De två cirklarna överlappar delvis
varandra. De båda utritade radierna bildar rät vinkel. Hur stor är
differensen mellan det röda och det blå området?
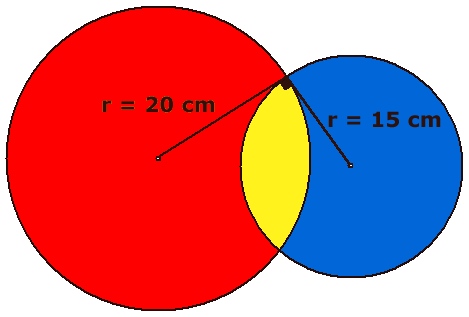 |
Metod 1:
Det går att räkna ut storleken av det röda och blå
området för att sedan räkna ut differensen mellan det röda och det blå
området. Men en så krävande arbetsinsats vill man naturligtvis undvika.
|
Metod 2:
Allmänt kan man säga att om cirkeln med radien 20 cm har arean A
cm2, cirkeln med radien 15 cm har arean B cm2
och det gemensamma området är C cm2, gäller
följande:
Det röda området är (A - C) cm2 och det blå området
är (B - C) cm2. (se figur) |
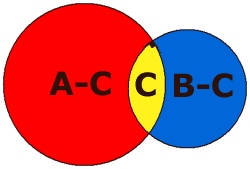 |
Differensen blir
då (A - C) cm2 - (B - C) cm2 = (A -
B) cm2 = (202
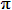 - 152
- 152
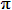 )
cm2 = 175 )
cm2 = 175
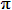 cm2
cm2
Anm.: Uppgiften om att radierna bildar rät vinkel
var således överflödig. |
|
Tillbaka
|
![]() ·
2 ·2 – 4(
·
2 ·2 – 4(![]() – 2) = 8.
– 2) = 8.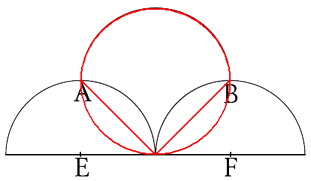




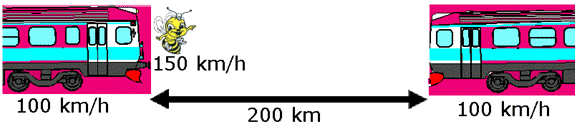
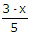 km, när det möter tåget första gången.
km, när det möter tåget första gången.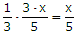 (km),
när biet vänder första gången.
(km),
när biet vänder första gången.