Almanacksalgebra!

Med hjälp av almanackan  kan man träna på att skriva algebraiska formler.

Ex. 1:
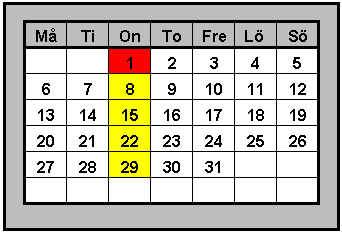
Utgå från talet i den röda rutan (talet 1 på rad 1). Uppgift: Skriv en  formel för talet i den gula rutan på rad n! Lösning: 1 + 7(n -1) som kan skrivas 7n - 6 Anm.: Om det första talet kallas a, blir den allmänna formeln a + 7(n - 1)

Ex. 2:
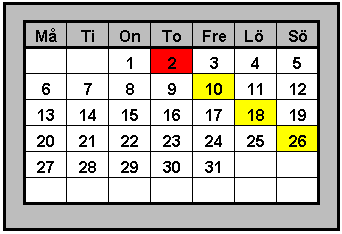
Utgå från talet i den röda rutan (talet 2 på rad 1). Uppgift: Skriv en  formel för talet i den gula rutan på rad n! Lösning: 2 + 8(n -1) som kan skrivas 8n - 6 Anm.: Om det första talet kallas a, blir den allmänna formeln a + 8(n - 1)

Ex. 3:
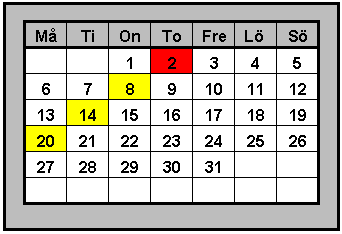
Utgå från talet i den röda rutan (talet 2 på rad 1). Uppgift: Skriv en  formel för talet i den gula rutan på rad n! Lösning: 2 + 6(n -1) som kan skrivas 6n - 4 Anm.: Om det första talet kallas a, blir den allmänna formeln a + 6(n - 1)

Ex. 4:
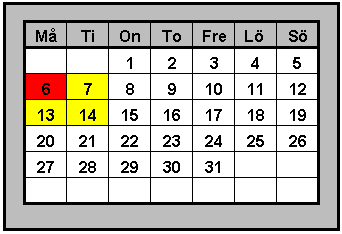
Utgå från talet i den röda rutan och bilda en rektangel (2x2 rutor) Uppgift: Skriv en  formel för summan av talen i denna rektangel! Lösning: Talet som vi utgår ifrån kallas a. Summan av talen blir då a + (a+1) + (a+7) + (a+8) Efter förenkling får vi 4a +16

Ex. 5:
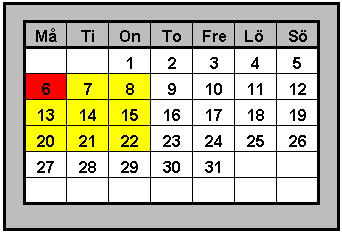
Utgå från talet i den röda rutan och bilda en rektangel (3x3 rutor)
Uppgift: Skriv en  formel för summan av talen i denna rektangel! Lösning: Talet som vi utgår ifrån kallas a. Summan av talen blir då a + (a+1) + (a+2) + (a+7) + (a+8)  + (a+9) + (a+14) + (a+15) + (a+16) Efter förenkling får vi 9a +72
Anm.: Om vi istället hade utgått från det mellersta talet på den översta raden och kallat det talet för x, hade vi fått en enklare formel: 18x

Ex. 6:
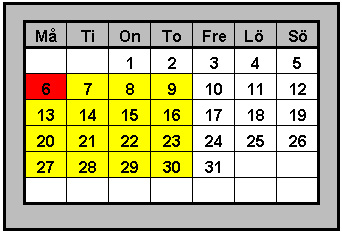
Utgå från talet i den röda rutan och bilda en rektangel (4x4 rutor)
Uppgift: Skriv en  formel för summan av talen i denna rektangel! Lösning: Talet som vi utgår ifrån kallas a. Med samma metod som i uppgift 4 och 5 får vi efter förenkling 16a + 192 Extrauppgift: Summan av talen i en annan rektangel (4x4 rutor) är 224. Visa att vi utgår från talet 2.
Pedagogiska idéer: 1. Utnyttja de framtagna formlerna för att lösa andra problem i almanackan. 2. Summan av talen i uppgifterna 4-6 kan naturligtvis beräknas med formeln för summan av den aritmetiska serien. Utgå gärna från figuren i uppg. 6, när du ska ge en rimlig förklaring till hur formeln ser ut.