Lätt:
Svar: En sexhörning
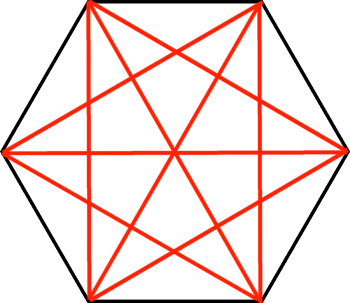
Lösning: Från varje hörn i en sexhörning kan man dra tre
diagonaler.
6 * 3 = 18.
Då har man räknat varje diagonal två gånger.
Därför måste vi dividera produkten med 2.
18/2 = 9.
Det går naturligtvis också att utnyttja formeln för antalet
diagonaler i en månghörning.
n(n-3)/2 = antalet diagonaler.
n =antalet hörn
n(n-3)/2 = 9 osv. |
 |
Medel:
Svar: 104 sidor.
Lösning:
Sid. 1- 9: 9 siffror
Sid. 10 - 99: 90 * 2 = 180 siffror.
Då återstår 204 - (9 + 180) = 15 siffror.
15 siffror räcker till fem tresiffriga tal, dvs. till talen
100, 101, 102, 103 och 104.
|

|
Svår:
Svar: Sidorna
förhåller sig som 3:4:5
(Egyptisk triangel)
Lösning:
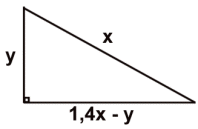
Antag att hypotenusan är x l.e. och att den ena kateten är y
l.e.
Summan av kateterna är 140 % av x, dvs. 1,4x
Den andra kateten är då (1,4x - y) l.e.
Pytagoras sats ger
y2 + (1,4x - y)2 = x2
Efter förenkling får man
y2 = 1,4xy - 0,48x2
Andragradsekvationen har lösningen
y = 0,7x ± 0,1x
y1= 0,8x
och 1,4x -y = 0,6x
y2= 0,6x och 1,4x -y = 0,8x
Båda lösningarna är med andra ord identiska.
Förhållandet mellan sidorna är 0,6:0,8:1
Det kan enklare skrivas 3:4:5 |
 |
|