Om man drar fem kort från en kortlek, kan man vara säker på att få minst två kort med samma färg (hjärter, ruter, klöver eller spader).
2.
Min assistent lägger därför undan ett kort av en färg, som förekommer mer än en gång.
3.
För att jag ska veta det dolda kortets färg, börjar min assistent med att visa ett kort med samma färg.
4.
Hur ska jag kunna lista ut det dolda kortets valör? Det finns
ju 12 kort kvar i färgen att välja på!
Svar: Det gäller att försöka hitta ett kodsystem, som ger mig
tillräcklig information.
Jag skulle kunna utnyttja, att min assistent kan variera
ordningsföljden för de återstående tre korten.
Det kan ske på sex olika sätt. (3! = 3*2*1 = 6)
Tolv kort men bara sex alternativ: Hur skall jag kunna komma
vidare??
William F. Cheney hittade en otroligt smart lösning:
Han placerade de 13 olika korten i en färg runt en cirkel med ess = 1, knekt = 11, dam = 12 och kung = 13
(se fig.)
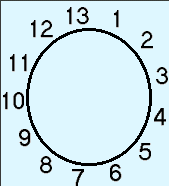
Det ger oss oanade möjligheter: Även om de två korten ligger så
långt ifrån varandra som möjligt på cirkeln, kan man nå det andra
kortet genom att medurs gå högst sex steg utmed cirkeln,
förutsatt att man startar på rätt kort!
Ex.: Antag att spader 2 och spader 9 finns bland de fem dragna
korten.
Vilket kort ska min assistent visa mig?
Svar: Spader 9, eftersom man kan komma till spader 2 på sex steg.
(Från spader 2 till spader 9 går det åt 7 steg.)
Ordningsföljden för de tre återstående korten kan enligt ovan varieras
på sex olika sätt. Utnyttja kortens valörer enligt följande metod:
ABC=1 steg ACB=2 steg BAC=3 steg BCA=4 steg CAB=5 steg
CBA=6 steg
A = minsta valören B = mellersta valören C = största valören.
Om två eller flera kort skulle ha samma valör, kan de t.ex. ordnas
efter färgerna hjärter, klöver, ruter och spader (ordnade efter
begynnelsebokstäverna.)
Ex.:
Min assistent visar mig ruter knekt och därefter spader 8, ruter 5 och klöver 6. Vilket är det dolda kortet?Lösning:
Färgen är ruter.
Valörerna för de tre återstående korten visas i ordning CAB=5 steg.
Jag startar på 11 (= ruter knekt) i cirkeln och fortsätt 5 steg medurs. Då hamnar jag på 3:an.
Det dolda kortet är alltså ruter 3.