Uppg. 1:
Svar:
400 cm
Lösning:
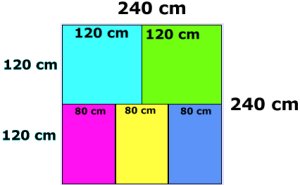
Den stora kvadratens sida:
960 cm/4 = 240 cm
Det kvadratiska badlakanet har sidan 240 cm/2 = 120
cm
Det rektangulära badlakanet
har kortsidan 240 cm/3 = 80 cm
och långsidan 240 cm - 120cm =
120 cm.
Omkretsen är då
2 . 120 cm + 2 .
80 cm = 400 cm
|
 |
|
|
Uppg. 2:
Svar:
Klassen består av 19 pojkar och 17 flickor
Lösning:
Vi gör följande antagande:
Flickor med glasögon: 9
Flickor utan glasögon: x
Pojkar med glasögon: x - 5
Pojkar utan glasögon: 2x
Ekvation: 9 + x + x - 5 + 2x = 36
4x = 32
x = 8
Antal pojkar: (8 - 5) + 2 . 8 = 19
Antal flickor: 9 + 8 = 17
|
|
|
Uppg. 3: |
|
|
Svar: 36 cm
Lösning:
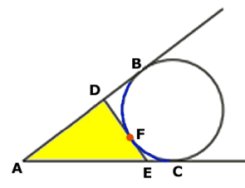
AB = AC (tangenter från punkten A) = 18 cm
Omkretsen av triangeln ADE =
Sträckorna AD + DF + FE + AE
Men DF = DB (tangenter från punkten D) och EF = EC (tangenter
från punkten E)
AD + DF + EF + AE kan därför skrivas
AD + DB + EC + AE = AB + AC =
2 . 18 cm = 36 cm (oberoende av var punkten F
ligger på den blå cirkelbågen BC) |
 |
|
Anm.:
Omkretsen av triangeln ADE påverkas inte av var punkten F ligger
på den blåfärgade cirkelbågen. |
|
|
Uppg. 4: |
|
|
Svar: n = 12
Lösning:
5! = 1 . 2 . 3
. 4 . 5 = 23 .
3 . 5 |
|
Hur många
5-faktorer innehåller 50! ?
Svar: 12 st (10 tal är delbara med 5. Dessutom innehåller 25 och
50 2 st
5-faktorer)
Finns det 12 st 23 i 50!, dvs. kan 50! delas upp i
36 st 2-faktorer?
Svar: Ja (25 st tal delbara med 2, 12 st tal delbara med 4, 6 st
tal delbara med 8 och 3 st tal delbara med 16 och 1 st tal
delbart med 32.)
(25 + 12 + 6 + 3 + 1) st 2-faktorer = 47 st 2-faktorer
Finns det 12 st 3-faktorer i 50! ?
Svar: Ja (16 st tal är delbara med 3, 5 st tal är delbara
med 9 och ett tal är delbart med 27)
(16 + 5 + 1) st 3-faktorer = 22 st 3-faktorer
Svar: Antalet 5-faktorer avgör att det högsta n-värdet är 12
|
|
|
Uppg. 5: |
|
a)
Svar:
15 kombinationer
Lösning:
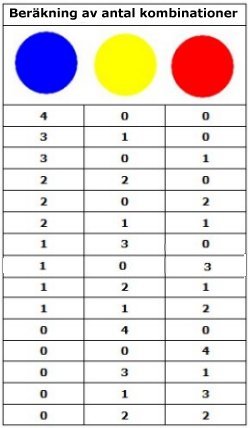
Det finns sammanlagt 15 kombinationer
OBS!
Antal kombinationer är
1 + 2 + 3 + 4 + 5 = 15
b)
Svar:
Antalet kombinationer när man tar n st brickor
blir 1 + 2 + ... + (n + 1)
Lösning:
Vi undersöker vad som gäller för de blå brickorna.
Om alla n brickorna är blå, finns det bara en kombination.
Om alla brickor utom en är blå, finns det 2 kombinationer.
......
Om ingen bricka är blå, finns det (n + 1) kombinationer.
Antalet kombinationer
blir 1 + 2 + ... + (n + 1)
Summan kan beräknas med formeln
(n + 1)(n + 2)/2
|
 |
|
Staffan R. har
föreslagit en elegant lösning:
Låt två väggar, l, placeras bland de fyra
brickorna. Kalla färgerna 1, 2 och 3.
Brickorna markeras med x.
|
xxxx ll
xxlxlx
xlxxlx
llxxxx
osv. |
 |
1111
1123
1223
3333 |
|
För n
st brickor gäller två lägen för väggarna bland (n +
2) platser
Vi får då
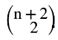 kombinationer. kombinationer.
För n=4 blir antalet kombinationer
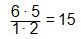
Antalet kombinationer kan också skrivas
(n+2)(n+1)/2. |
|
|