|
den nya renen |
|
|
|
kvadraterna |
Svar:
a) 40 tändstickor
b) 2n(n + 1)
Lösning:
a)
Antalet vågräta tändstickor är 4 . 5
Antalet lodräta tändstickor är 4 . 5
Sammanlagt 2 . 4 . 5 = 40
b)
I uppgift a är n = 4
Om vi i uppgift a byter ut 4 mot n och
5 mot (n + 1) får vi formeln 2n(n + 1)
|
 |
Extrauppgift
Svar: 12 + 22 + 32...+
n2
Lösning:
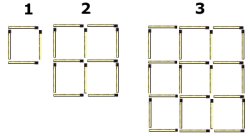
I fig. 1 finns en kvadrat. Det kan skrivas 12
(kvadraten har ett läge vågrätt resp. lodrätt, dvs. 12)
I fig. 2 finns 1 + 4 = 5 kvadrater.
Det kan skrivas 12 + 22
I fig. 3 finns 1 + 4 + 9 = 14 kvadrater
Det kan skrivas 12 + 22 + 32
I figur n finns 12 + 22 +
32...+ n2
Denna summa kan beräknas med formeln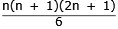
Testa gärna formeln i fig. 1, 2 och 3. |
 |
|
|
|
miniräknaren |
Bevis:
Vi kallar talen i kvadraten för
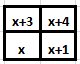
Vilken tangent vi än startar med, gäller att summan av första och tredje siffran
i talet är lika med summan av andra och fjärde siffran i talet.
Betyder det att det fyrsiffriga talet är delbart med 11?
Vi undersöker vad som händer om vi multiplicerar ett tresiffrigt tal med
siffrorna a, b och c med 11.
Utför multiplikationen
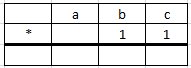

Slutsats: Om
summan av första och tredje siffran i talet är
lika med summan av andra och fjärde siffran i talet, är talet jämnt
delbart med 11. |
Ett exempel på att de fyra siffrorna i
en kvadrat på tangentbordet bildar ett tal som är delbart med 11:
Första tangent: x+3
Alt. 1: Talvärde: 1000(x+3)+100(x+4)+10(x+1)+x =1111x+3410 =11(101x +310)
Alt. 2: Talvärde: 1000(x+3)+100x+10(x+1)+x +4 =1111x+3014 =11(101x +274)
|
|
|
|
stolparna |
Svar: Stolparna berör inte varandra
Lösning:
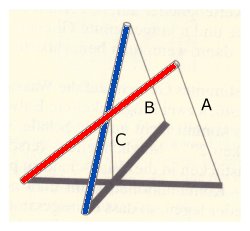
Solstrålarna A och B är parallella.
Om de båda stolparna berör varandra, måste en ljusstråle (C) från
beröringspunkten till skärningspunkten av skuggorna vara parallell med A och
B.
I figuren ser vi att så inte är fallet.
Stolparna berör inte varandra.
(Problemet finns i Heinrich Hemme:
Der Wettlauf mit der Schildkröte) |
 |
|
|
a merry christmas |
Svar: 9 34225 7396 81 900
Lösning:
A MERRY XMAS TO ALL
TO:
Här finns det två alternativ:
36 T = 3 och O = 6
81 T = 8 och O = 1 |
ALL:
Här finns det fyra alternativ:
100 A = 1 och L = 0
144 A = 1 och L = 4
400 A = 4 och L = 0
900 A = 9 och L = 0 |
XMAS
Här finns det 13 alternativ:
1521, 1681, 2025, 3364, 3481, 4489, 4624, 5776, 5929, 7225,
7396, 8836, 9025
Jämför ALL och XMAS
Tiotalssiffran i XMAS
måste vara 1, 4 eller 9. Det enda tal som uppfyller det
villkoret är 7396.
XMAS =
7396.
Då är A= 9 och
ALL = 900.
TO = 81 (M = 3 enligt XMAS.
Då kan
inte TO = 36)
|
MERRY
Här finns det fem alternativ:
14884, 27556, 34225, 52441, 61009
MERRY = 34225 (Eftersom M =
3)
Problemet finns i Charles W. Trigg:
Mathematical Quickies |
|
|
|
|