Baltic Way - en landskamp i matte för gymnasieelever (lösning)
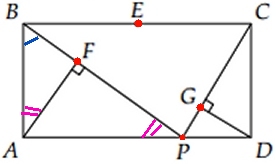
Trianglarna ABP och ABF är likvinkliga och därför likformiga.
BF/AB = AB/BP
BF . BP = AB2
Men AB = BE.
Då kan vi istället skriva BF . BP = BE2
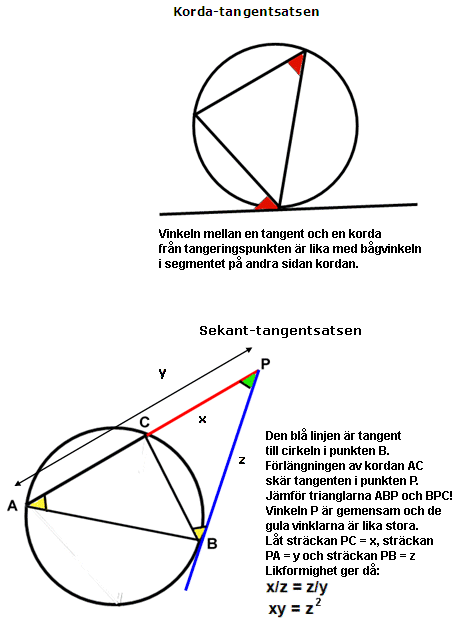
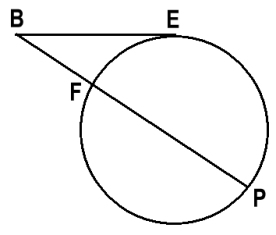
Genom att tillämpa sekant-tangentsatsen kan vi konstatera att det finns en cirkel, som går genom punkterna E, F och P (se figur nederst till höger)
På motsvarande sätt kan vi visa att det finns en cirkel, som går genom punkterna
E, G och P.
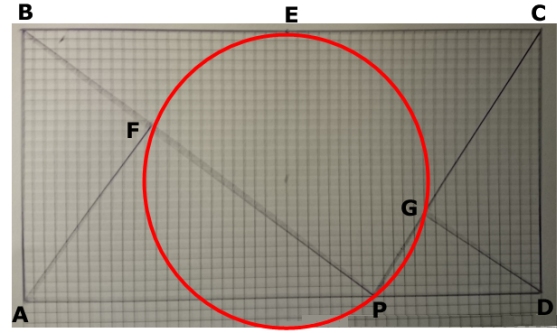
Eftersom det bara finns en cirkel, som går genom P och samtidigt tangerar sidan BC i E, har vi visat att punkterna E, F, P och G ligger på omkretsen till en cirkel.
 |