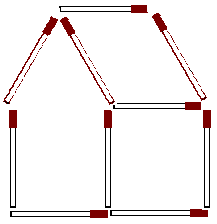
Klurigt nr 8 (lösningar)

Husgaveln 

Bokstavsproblem

Bokstaven F (upp och nervänd)

Påskäggen

Erik har fått i uppgift att koka påskäggen i 7 minuter. Han har två timglas, som visar tiden 5 resp. 3 minuter. Hur skall han göra? Lösning: 1) Vänd båda timglasen samtidigt. 2) När 3 min-timglaset runnit ut, vänds detta på nytt. 3) När 5 min-timglaset runnit ut, har 3 min-timglaset runnit i 2 min. 4) Vänd 3 min-timglaset på nytt, så tar det 2 min för det att rinna ut.  5 min + 2 min = 7 min

Vasaloppet

En lösning skulle kunna se ut så här. a) Antag att professor Kalkyl har x km kvar till målet. Ekv.:          x = 30 Svar: Professor Kalkyl skulle snart vara framme vid kontrollen i Oxberg. b) Med ledning av ekvationen ovan inser man att klockan måste vara 13.00. Eftersom loppet (90 km enligt banprofilen) startar kl. 08.00 har han kört 60 km på 5 timmar, dvs. hans medelhastighet har varit 12 km/h. Det är därför knappast troligt att professor Kalkyl skulle kunna öka hastigheten i slutet av loppet, speciellt som banprofilen visar att han redan passerat det mest lättåkta partiet (efter Evertsberg). Å andra sidan skulle det kunna finnas faktorer som talar för en högre snitthastighet de tre sista milen: 1) Professor Kalkyl kan ha stått i ett av de sista startleden och då kan det ha varit svårt att passera långsammare skidåkare, speciellt i den trånga passagen efter starten. I Oxberg ligger han förmodligen på en placering mellan 4000 och 5000. I så fall är det lättare för honom att hålla sitt eget tempo de sista milen. 2) Om det var mycket kallt vid starten, var säkert föret kärvt under morgonen och förmiddagen. Det går troligen att köra fortare, när temperaturen stigit. 3) Naturligtvis är det mycket stimulerande att närma sig målet i Mora. Kanske kan det ge professor Kalkyl extra krafter.

Resan till Blåkulla

En lösning kan se ut så här: Årets hastighet är 5/6 av fjolårets hastighet Û   fjolårets hastighet är 6/5 av årets hastighet. Antag, att hastigheten det här året var x km/h. Sträckan betecknas med a km Förra året kom häxan till Blåkulla kl. 22.22. I år anlände hon kl. 23.32. Förra året gick alltså resan 70 min (7/6 h) snabbare. Ekv.:            x = a/7

Eftersom bränslet räckte för ca 640 km och marginalerna var små, bör avståndet till Blåkulla ha varit obetydligt kortare, kanske 630 km. I så fall blir hastigheten 630/7 km/h = 90  km/h

Primtal I

Senast de tre siffergrupperna i ett datum bestod av tre primtal var den 29 november 1997 (97-11-29).

Primtal II

Förutsättning: Talet n är ett primtal. Påstående: n2 -1 är delbart med 24, om n är ett primtal >3 Bevis:  n2 - 1 = (n+1)(n-1) n -1, n och n +1 är tre på varandra följande heltal på tallinjen 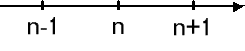Eftersom n är ett primtal, är det ett udda tal. Då är såväl n -1 som n +1 jämna tal, dvs. jämnt delbara med två. Vartannat jämnt tal är dessutom jämnt delbart med fyra.  Vart tredje tal är  jämnt delbart med tre. Eftersom n är ett primtal, måste det vara n - 1 eller n + 1 som är jämnt delbart med tre. Av ovanstående resonemang framgår att  (n+1)(n-1) innehåller faktorerna 2, 3 och 4, dvs. produkten är 24. V.S.B.

Tomten

Summan av alla siffrorna före avstyckningen måste vara mindre än 102. Summan av alla siffrorna t.o.m. tomt   nr 18 blir 90.   Duger inte. nr 19 blir 100. Duger!   102 - 100 = 2 nr 20 blir 102. Duger inte.   Svar: Det finns två möjligheter. Antingen är det tomt nr 2 eller är det tomt nr 11. Det återstår inget annat för Berg än att kontakt den koleriske stadsarkitekten för att få ytterligare upplysningar.

 

|Tillbaka|