Månadens problem
oktober 2020
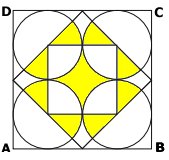
Uppg. 1
Hur stor del av kvadraten ABCD är färgad gul?		  
Uppg. 2:      
Palindromer
Talen 66 och 828 är exempel på två palindromer, som är delbara med 6.
Uppgift: Hur många palindromer mellan 1000 och 10000 är delbara med 6?
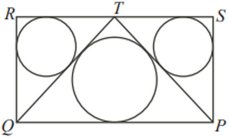
Uppg. 3:
T är mittpunkt på sidan RS i rektangeln PQRS.
Den större cirkeln har radien 4 cm och de båda mindre cirklarna har radien 3 cm.
Beräkna rektangelns sidor.
Uppg. 4:
Låt a och b vara reella tal med a>1 och b>0.
Bestäm värdet på a, när ab= ab och a/b = a3b.
 
Uppg. 5:
I en skål ligger ett antal glaskulor.
Adam, Britta och Cissi tar i tur och ordning en eller två kulor från skålen.
Adam börjar, sedan Britta och sedan Cissi. Därefter Adam osv.
Den som tar den sista kulan förlorar.
 
a) Kan Britta och Cissi samarbeta och tvinga Adam att förlora, när det från början
finns 5 kulor i skålen?
b) Antag att det finns N kulor i skålen från början. För vilka värden på N kan Britta och Cissi tvinga Adam att förlora, om de samarbetar?


Du kan mejla din lösning till mig (alf@mathpuzzle.se)
Pelle P. och Staffan R. har skickat lösningar.

 Lösningar  Tillbaka