|
Månadens
problem |
Problem för hängmattan
och badstranden |
||
|
Uppg. 1: På en gata finns det tio lyktstolpar utplacerade med jämna mellanrum, varav en lyktstolpe finns i början av gatan och en finns i slutet. På en annan gata finns det
100 lyktstolpar placerade på samma sätt som på den första gatan.
|
 |
|
|
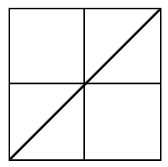
Uppg. 2: a) Hur många trianglar resp. kvadrater finns det i figuren till höger? b) Vilket är förhållandet mellan trianglarnas och kvadraternas sammanlagda areor? |
 |
|
|
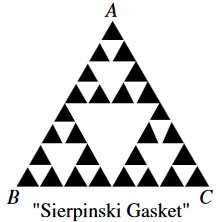
Uppg. 3: Hur stor del av triangeln ABC är svart? Anm.: Detta är en fraktal, som beskrevs av Sierpinsky 1915. Liknande mosaikmönster fanns dock redan på 1200-talet i Italien. |
 |
|
Uppg. 4:
|
||
|
Uppg. 5: x, y och w är positiva heltal. Beräkna värdet av x, y och w med hjälp av ekvationen till höger. |
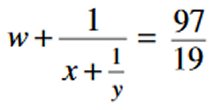 |
|
|
Uppg. 6: En Mercedes Van med hastigheten 100 km/h och en Kia med hastigheten 80 km/h är på väg till Alphaville. Mercedes Van kör om Kia:n 10 minuter innan Kia:n är framme i Alphaville. Hur mycket senare kommer Kia:n till Alphaville jämfört med Mercedesbilen?
|
  |
|
|
Uppg. 7: A och B är positiva heltal Bestäm deras värde med hjälp av algoritmen till höger. |
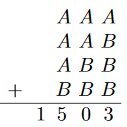 |
|
|
Uppg. 8: När en bonde skulle programmera sitt fyrsiffriga kodlås till ett av uthusen, bestämde han att den tredje siffran skulle vara 4 samt att alla fyra siffrorna skulle vara olika. Dessutom skulle siffrorna bilda ett tal, som var jämnt delbart med 45. Hur många olika kombinationer fanns det då? |
 |
|