|
det var bättre förr!? Del 4 |
Efter
de deprimerande PISA-rapporterna är det intressant att se
svårighetsgraden på ett par
uppgifter från 1944: Övningsexempel i matematik för realgymnasiet,
R
I3 (Bengt Lindvall). |
Ex. 1:
På AB som diameter uppritas en cirkel. Sök avståndet från A
till en punkt C på cirkelns periferi, när C ligger lika långt
från A som från tangenten genom B.
Cirkelns radie är 2 dm. |
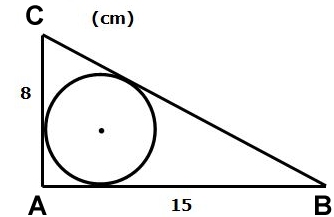
Ex.
2:
I en rätvinklig triangel med
kateterna 8 cm och 15 cm viker man upp alla tre hörnen, så att
deras spetsar möts i den inskrivna cirkelns medelpunkt.
Beräkna arean av var och en av de delar av triangeln, som inte
blir övertäckta vid vikningen. |
 |
|